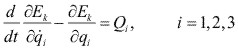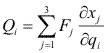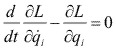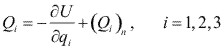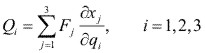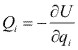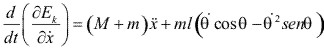5.5.- FORMA BÁSICA DE LAS ECUACIONES DE LAGRANGE
5.5.1.1 Ligaduras o Vínculos.
Se denominan ligaduras a cualquier sistema material capaz de impedir o condicionar el libre movimiento de una partícula o cuerpo, siendo independientes de las fuerzas actuantes, es decir, son condiciones que restringen el movimiento de una partícula o sistema de partículas, reduciendo el número de grados de libertad con respecto al caso en que todas las partículas fueesen libres.
Si una partícula no tiene ninguna limitación en su movimiento, decimos que se trata de un partícula libre en cuyo caso, para fijar o determinar su posición, será necesario fijar tres coordenadas, por ejemplo, x, y, z. Decimos entonces que la partícula libre tiene 3 grados de libertad en el espacio y 2 si se mueve en un plano.
En cambio, si la partícula esta sujeta a algún tipo de restricción o de limitación en su movimiento, decimos que la partícula está vinculada. El medio mediante el cual se provoca la limitación o restricción, se llama vínculo o ligadura. Se llama vínculo bilateral (o reversible) a aquel en que el punto está permanentemente en contacto con el vínculo, por ejemplo, una partícula que se mueve dentro de un tubo. En el presente texto, sólo haremos referencia a este tipo de vínculo; la que explicaremos líneas abajo.
Por extensión, decimos que un sistema de partículas o en general, un cuerpo, están vinculados, cuando no se pueden mover libremente, en el plano o en el espacio, si no que están sujetos a ligaduras.
Podemos citar los siguientes ejemplos, que estudiaremos:
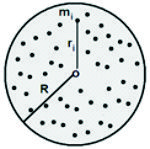
Para F5-5.5.1.1(a) el efecto de la fuerza desconocida es mantener la masa a la distancia del origen O, haciendo que el movimiento de la masa esté restringido. Cuando ocurre esto, se dice entonces que la masa está sometida a una ligadura y a la fuerza que restringe su movimiento (la ejercida por la cuerda) se le llama fuerza de ligadura.
Una partícula obligada a moverse sobre una determinada curva, por caso, un anillo impulsado con cierta velocidad inicial en una guía, recta o curvada o una esfera dentro de un tubo. El vínculo es la guía, Figura F5-5.5.1.1(b).
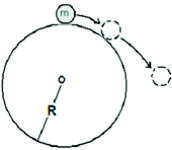
Una partícula de masa m el extremo de una cuerda inextensible, que rota con velocidad uniforme, en un plano horizontal liso. La cuerda obliga a la partícula a describir una trayectoria circular, Figura F5-5.5.1.1(c).
Una varilla uno de cuyos extremos está obligado a moverse sobre el eje y y el otro sobre el eje x, F5-5.5.1.1(d).
Un disco que rueda sobre una recta en un plano inclinado. El vínculo es el plano inclinado, F5-5.5.1.1(e).
Una semiesfera a la que se apoye sobre un plano horizontal y se la deja caer. El vínculo se supone que es una línea recta. Ver en la F5-5.5.1.1(f), casos de plano liso y de plano rugoso.
Una barra, articulada en su extremo izquierdo y con su otro extremo libre, que se la suelta desde la posición horizontal, F5-5.5.1.1(g).
En la F5-5.5.1.1(h), en A, la varilla apoya sobre un rodillo, lo que le permite deslizar sin rozamiento. En este caso, la fuerza que el vínculo ejerce sobre la varilla, es perpendicular a ésta. Dicha fuerza no puede tener componente en la dirección de la varilla: esto es así, porque la ausencia de rozamiento impide que el rodillo transmita a la varilla una fuerza que no sea en la dirección normal a esta última.
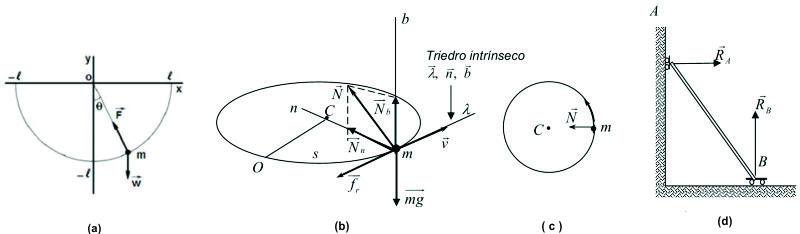
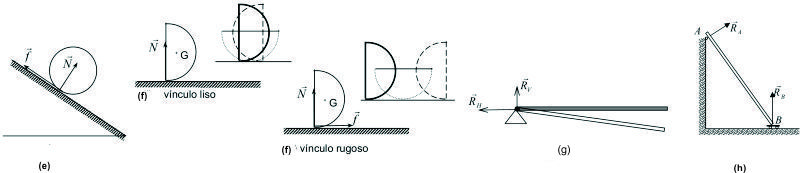
Figura F5-5.5.1.1
a).- Algunas ecuaciones de ligaduras en sistemas sencillos:
|
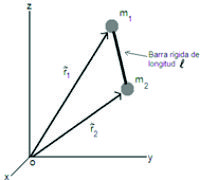
i).- En el caso de un bloque que se desliza sobre un plano inclinado, dicho bloque está obligado a moverse sobre el plano (ver figura F5-5.5.1.2) y la ligadura puede expresarse como:
ii).- El péndulo de la figura F5-5.5.1.1(a), está obligada a moverse en una trayectoria semicircular. En este caso la ligadura se puede expresar como:
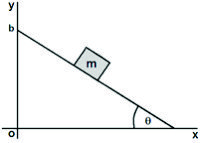
iii).- En un cuerpo rígido (ver figura F5-5.5.1.3 y figura F5-5.5.1.4) las partículas están enlazadas de manera que la distancia entre ellas permanece constantes, pudiéndose establecer la ligadura como:
|
Figura F5-5.5.1.2.- Un bloque de masa m que se mueve sobre una superficie inclinada. |
|
Figura F5-5.5.1.3.- Cuerpo rígido.
|
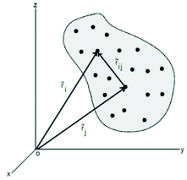
Figura F5-5.5.1.4.- Dos masas m1 y m2 unidas por una barra rígida de longitud
|
b).- Clasificación de ligaduras.- Las ligaduras se pueden clasificar de varias formas, a continuación algunas de ellas:
|
i).- Si son o no desigualdades:
Dependen de las ecuaciones de ligadura, estás describen los efectos de la fuerza, es decir, sus implicaciones sobre la dinámica del sistema al que se aplique una determinada fuerza.
*).- Unilaterales.- Se dice que una ligadura es unilateral cuando son expresadas mediante una desigualdad.
Ejemplo de algunas ligaduras unilaterales:
**).- Bilaterales(o reversibles).- Se da cuando el sistema o cuerpo está permanentemente en contacto con el vínculo, luego se dice que una ligadura es bilateral cuando se expresa mediante una igualdad. Este tipo de ligaduras pueden escribirse en la forma general:
El subíndice l indica que puede haber más de una ligadura de este tipo en el sistema, siendo m el número total de ellos.
Ejemplo de algunas ligaduras bilaterales, están dadas en las ligaduras dadas por las figuras F5-5.5.1.3 y F5-5.5.1.4.
ii).- Si dependen explícitamente o implícitamente del tiempo:
*).- Ligaduras reónomas.- Se dice que una ligadura es reónoma si depende explícitamente del tiempo. También se les llaman ligaduras móviles.
Ejemplo de algunas ligaduras reónomas:
**).- Ligaduras esclerónomas.- Se dice que una ligadura es esclerónoma si no depende explícitamente del tiempo. También se les llaman ligaduras fijas o estacionarias.
Por otro lado, si un sistema tiene todas sus ligaduras esclerónomas entonces se dice que el mismo es esclerónomo, pero si al menos una de sus ligaduras no lo es entonces se dice que es reónomo. Ejemplo de algunas ligaduras esclerónomas:
Las ligaduras expresadas por las figuras: F5-5.5.1.3, F5-5.5.1.4, F5-5.5.1.5 y F5-5.5.1.6 son ligaduras esclerónomas.
iii).- Por su integridad:
*).- Ligaduras holónomas o geométricas.- Decimos que un sistema es holónomo, si no tiene vínculos, o bien , si los tiene, éstos son expresables mediante m ecuaciones finitas en los parámetros de Lagrange. Mediante estas m ecuaciones finitas, podemos obtener m parámetros del sistema en función de los otros (n - m) parámetros que hemos tomado como independientes.
En ese caso, siempre será posible considerar el sistema como si fuese un sistema libre, sin vínculos, pero que, en vez de tener 3N grados de libertad, tuviese h = 3N - m grados de libertad.
En un sistema holónomo, la cantidad de parámetros o coordenadas necesarios para configurar el sistema, coincide con la cantidad de grados del libertad del mismo.
Luego son ligaduras bilaterales que no dependen de las velocidades, sólo dependen de las posiciones de las partículas y el tiempo, exclusivamente. Son integrables, por lo tanto, es posible emplearlas para eliminar las coordenadas dependientes puesto que expresan relaciones algebraicas entre las coordenadas.
Este tipo de ligaduras son geométricas (curvas, superficies, etc.) y se pueden escribir en la forma:
Ejemplo de algunas ligaduras holónomas:
Las ligaduras expresadas por las figuras: F5-5.5.1.3, F5-5.5.1.4 y F5-5.5.1.5
**).- Ligaduras no-holónomas.- Decimos que un sistema es no holónomo o anholónomo si una, o más, de las m relaciones de vínculo, está expresada como una ecuación diferencial no integrable.
Si la ecuación diferencial que expresa el vínculo fuese integrable, dicha expresión se transformaría en finita y el sistema pasaría a ser holónomo. Es importante hacer notar que, si el sistema es anholónomo, no es posible encontrar los m parámetros de configuración en función de los restantes.
En este tipo de sistemas, la cantidad de grados de libertad sigue siendo h, pero es posible demostrar que ya no resultan suficientes h parámetros para configurar el sistema, sino que para ello son necesarios (h + r) parámetros, en donde r es la cantidad de ecuaciones de vínculo que no son integrables.
Es posible demostrar asimismo, que este tipo de sistema se tiene cuando existen líneas o superficies que ruedan sin resbalar sobre superficies, como es el caso de una esfera que rueda sin deslizamiento sobre un plano. En cambio, cuando la rodadura se hace sobre una línea y no sobre un plano, el sistema es holónomo.
Si en un sistema al menos una de las ligaduras es no-holónoma, se dice que el sistema es no-holónomo.
Todas las ligaduras unilaterales son de este tipo. Puede haber ligaduras bilaterales no-holónomas. Un caso particularmente importante de este tipo de ligadura lo constituyen aquellas que pueden ser expresadas en términos de las velocidades de las partículas en el sistema, es decir:
Estas constituyen ligaduras no-holónomas, a menos que la ecuación pueda ser integrada para encontrar relaciones entre las coordenadas. Debido a que algunas veces pueden ser integrables y convertirse en holónomas, a las ligaduras del tipo, suelen llamárseles semi-holónomas.
Ejemplo de algunas ligaduras no-holónomas.
|
5.5.1.2.- Fuerza de ligadura o Reacción de vínculo.
Fuerza de ligadura son las responsables de las restricciones del sistema y aparecen espontáneamente al establecer una ligadura y aseguran su cumplimiento. Actúan tanto si el sistema está en reposo o si está en movimiento, a priori son desconocidas a diferencia de las fuerzas aplicadas, no puede ser determinada sin conocer las otras fuerzas que actúan.
Cuando una partícula se mueve sobre un vínculo, éste ejerce sobre aquella una fuerza que se llama fuerza de ligadura o reacción de vínculo. De la misma forma, en el movimiento de un cuerpo vinculado, la fuerza de vínculo aparece en el punto, o en la superficie de contacto del cuerpo con el vínculo. Está aplicada en el cuerpo. El término “reacción” se usa por costumbre. También podría usarse el término “acción” para designar la fuerza que el vínculo ejerce sobre el cuerpo. Adoptaremos: “reacción de vínculo”, para designar la fuerza aplicada en el cuerpo, que le es ejercida por el vínculo.
En algunos casos, resulta cómodo decir que la dirección en que ocurre esa fuerza es la dirección en la que el vínculo impide o restringe el desplazamiento del cuerpo.
En la figura F5-5.5.1.1(b) se muestran las componentes de la reacción de vínculo en un anillo que semueve (impulsado con una velocidad inicial) sobre una guía curva, en un plano horizontal. Hay componentes de la reacción de vínculo en las 3 direcciones del triedro intrínseco: En la dirección de la tangente, está la fuerza de rozamiento. En la dirección de la normal, está la fuerza centrípeta que el anillo ejerce sobre la partícula y en la dirección de la binormal, se tiene la reacción del peso del anillo.
En la figura F5-5.5.1.1(c) se tiene una partícula que describe un movimiento circular uniforme en un plano horizontal liso, obligada a ello por un segmento rígido (supuesto sin masa) rotante, o por una cuerda inextensible. La fuerza de vínculo que ejerce la cuerda, pasa por el centro de rotación (también se tiene la reacción del plano, que no está dibujada).
En la figura F5-5.5.1.1(d) se tiene una varilla uno de cuyos extremos está obligado a moverse sobre el eje y y el otro sobre el eje x, sin rozamiento. Las reacciones son perpendiculares a cada dirección.
En la figura F5-5.5.1.1(e) se tiene un disco que rueda sin resbalar sobre una recta en un plano inclinado. En el punto de contacto del disco sobre el plano, se tienen 2 componentes de la fuerza de vínculo: una componente normal, que corresponde a la componente del peso del disco en esa dirección. La otra componente se indica con ![]() y corresponde a la fuerza de rozamiento estático, debida a la rugosidad de las superficies que impide que el disco deslice sobre el plano. Los sucesivos puntos de contacto discoplano, considerados como puntos del disco, tienen, en cada instante, velocidad cero.
y corresponde a la fuerza de rozamiento estático, debida a la rugosidad de las superficies que impide que el disco deslice sobre el plano. Los sucesivos puntos de contacto discoplano, considerados como puntos del disco, tienen, en cada instante, velocidad cero.
En la figura F5-5.5.1.1(f) se muestra una semiesfera, la que se apoya inicialmente sobre un plano horizontal rugoso y luego se la suelta y donde se supone que el vínculo es una recta del plano. El peso de la esfera produce un momento con respecto al punto de contacto, lo que lleva a situaciones diferentes, según que el vínculo sea, o no, liso, como veremos seguidamente.
Si el vínculo es perfectamente liso, ese momento hace girar la semiesfera, la cual desliza sobre el punto de apoyo. No hay fuerza externa en la dirección horizontal y entonces: el centro de masas desciende con trayectoria vertical hasta alcanzar su punto más bajo, de energía potencial mínima y luego sube nuevamente hasta que la semiesfera quede en una posición simétrica a la inicial. A partir de allí se reinicia el ciclo, y se tiene un movimiento oscilatorio.
En cambio, si la rugosidad del vínculo impide el deslizamiento de la esfera sobre la recta del plano, los sucesivos puntos de contacto esfera - recta del plano, tienen, en cada instante, velocidad cero.
En este caso, aparece una componente horizontal de la fuerza de vínculo, la que provoca que el vector aceleración del centro de masas tenga una componente hacia la derecha. Finalmente, la semiesfera también adquirirá un movimiento oscilatorio pero, a diferencia del caso anterior, el vector aceleración del centro de masas, tendrá componente en la dirección horizontal, debida a la componente en esa dirección de la fuerza de vínculo (teorema del movimiento del centro de masas).
En la figura F5-5.5.1.1(g) se tiene una barra articulada en un extremo, que inicialmente se la sostiene en la posición horizontal y luego se la suelta. La dirección de la reacción va cambiando a medida que la barra cae. Sólo en el instante inicial y cuando la barra pasa por la posición vertical la reacción es vertical.
En las posiciones intermedias la reacción tendrá una componente RH y una componente RV.
En la figura F5-5.5.1.1(h), en A, la varilla se apoya sobre un rodillo, lo que le permite deslizar sin rozamiento.
En este caso, la fuerza que el vínculo ejerce sobre la varilla,es perpendicular a ésta. Dicha fuerza no puede tener componente en la dirección de la varilla: esto es así, porque la ausencia de rozamiento impide que el rodillo transmita a la varilla una fuerza que no sea en la dirección normal a esta última.
Una condición adicional que se imponen a las fuerzas de ligadura es que puedan ser tan grandes en magnitud como fuera necesario para imponer la ligadura, lo que es una idealización de las ligadura reales, pues los hilos se estiran, las varillas se doblan o se quiebran, etc., pero se trabaja dentro de los límites en lo que esto no pasa o su efecto puede despreciarse.
Nota.- La fuerza aplicada es aquella determinada independientemente de cualquier otra fuerza, dando sólo las posiciones (y a veces también las velocidades) de las partículas.
5.5.1.3.- Determinación de la posición de un sistema de partículas, parámetros de configuración con vínculos fijos (sistema esclerónomo).
Se llama configuración de un sistema a la posición de cada una de sus partículas en un instante dado. Para definir la configuración se necesita un determinado número de parámetros, según el sistema de que se trate. Por ejemplo, una partícula libre precisa tres parámetros: las coordenadas cartesianas, (x; y; z). Un sistema de n partículas libres queda definido por 3n parámetros. Sin embargo, si existen ligaduras que restrinjan el movimiento, el número de parámetros preciso para definir la configuración será menor. Se denominan grados de libertad de un sistema al conjunto mínimo de parámetros necesario para definir unívocamente la configuración del mismo, y que puedan variarse de manera independiente (es decir, sin ecuaciones de ligadura).
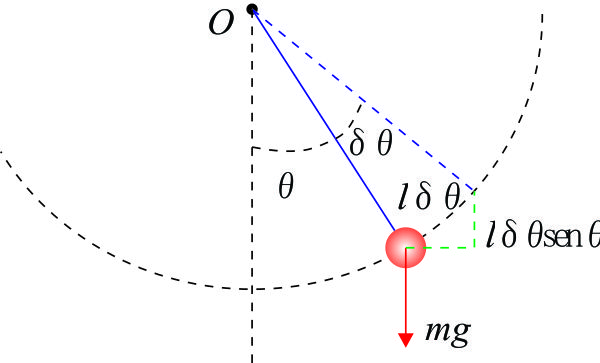
Ahora bien: puede ocurrir que algunos puntos del sistema estén vinculados entre sí, por ejemplo: 2 masas puntuales libres en el plano, suman 4 grados de libertad y hacen falta 4 coordenadas para configurar el sistema. Pero supongamos que las dos partículas estén vinculadas entre sí por un segmento inextensible de longitud l: en este caso bastará fijar las 2 coordenadas de una de ellas más el ángulo que forma el segmento con la horizontal, en total 3 coordenadas independientes entre sí, para tener determinado el sistema. Ciertamente, esta restricción de vínculo, se podrá establecer mediante una determinada ecuación que deberán satisfacer las coordenadas. Esa ecuación es:
![]()
Se llaman parámetros de configuración, o coordenadas de Lagrange, a las coordenadas que se usan, o que se pueden usar, para configurar un sistema. Decimos, que se pueden usar, porque, en realidad, la posición de las dos masas acopladas por una barra, queda definida también usando los 4 parámetros x1 x2 x3 x4, aunque si la definimos así, estaríamos usando un parámetro superabundante:
Llamaremos por lo tanto parámetros de Lagrange a todas las coordenadas de configuración, ya sean estas superabundantes o ya sean independientes. Designaremos con qk a estos parámetros, con k = 1,2,3,... n.
De acuerdo con el ejemplo que se ha mostrado, resulta entonces, que, si los parámetros de configuración deben satisfacer una ecuación de vínculo, eso hace que el sistema se configure con 3, en vez de con 4 parámetros.
Hablando en general, si llamamos n a la cantidad de parámetros de Lagrange y m a la cantidad de ecuaciones que representan las restricciones de vínculo, podemos expresar:
Cantidad de parametros independientes = n - m
Luego las restricciones limitan la configuración geométrica y el movimiento del sistema. Una restricción genera reacciones y disminuye el número de grados de libertad del sistema.
Si llamamos (Pi - O) al vector posición de una partícula i del sistema, podemos expresar finalmente la configuración de un sistema de partículas mediante la siguiente función vectorial:
|
[5.1.1.01]
|
Con k = 1,2,3,.... (n - m), en donde los qk son parámetros independientes entre sí. Cada uno de estos parámetros es función del tiempo.
También podemos expresar, en forma escalar, las coordenadas de posición xi , yi , zi de una partícula i del sistema, en función de los (n - m) parámetros independientes:
|
[5.1.1.02]
|
Con k = 1,2,3,.... (n - m)
Si N es la cantidad de partículas del sistema tendremos 3 N ecuaciones como las [5.1.1.02] que nos permitirán conocer las coordenadas de cada una de las N partículas en función de los parámetros qk independientes. Entonces podemos llamar a las [5.1.1.01] o [5.1.1.02], ecuaciones de transformación, porque nos permiten pasar de los parámetros de configuración, a las coordenadas de posición de las partículas. También podríamos designarlas como ecuaciones de configuración.
Debemos observar que en las [5.1.1.01] y [5.1.1.02], no aparece el tiempo en forma explícita: ello significaque si bien las coordenadas xi , yi , zi dependen del tiempo, lo hacen a través a través de las qk.
Esta no dependencia en forma explícita del tiempo, se debe a que hemos considerado que los vínculos permanecen fijos en el tiempo, por ejemplo, si un punto se mueve sobre una curva en el espacio, esa curva no cambia su forma con el tiempo, entonces, si dejamos constante un valor del parámetro (por ejemplo ese parámetro podría ser el arco ó recorrido de la partícula sobre la curva), la posición de la partícula no cambia porque la curva no se mueve.
Veamos el siguiente ejemplo, figura F5-5.5.1.7: Una partícula P se mueve en un plano sujeto a un vínculo tal que su distancia al punto “O” es constante e igual a l, figura F5-5.5.1.7.
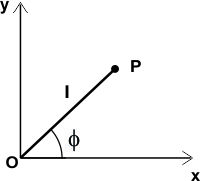
Figura F5-5.5.1.7
Los parámetros de Lagrange son q1 = x ; q2 = y y la ecuación de ligadura es q12 + q22 - l2 = 0.
Podemos tomar como parámetro independiente q1, en cuyo caso q2 es superabundante, porque podemos obtenerlo con la ecuación de ligadura.
También podemos tomar como parámetro independiente al ángulo ![]() en cuyo caso q1 y q2 pasan a ser superabundantes. Si consideramos los 3 parámetros q1 , q2 y
en cuyo caso q1 y q2 pasan a ser superabundantes. Si consideramos los 3 parámetros q1 , q2 y ![]() , (n = 3) podremos establecer entre ellos 2 ecuaciones de ligadura (m =2), de manera que la cantidad de parámetros independientes siempre será 3 - 2 = 1.
, (n = 3) podremos establecer entre ellos 2 ecuaciones de ligadura (m =2), de manera que la cantidad de parámetros independientes siempre será 3 - 2 = 1.
Las ecuaciones de transformación que dan las coordenadas de la partícula en función del parámetro ![]() son:
son:
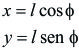
Donde ![]() es una cierta función del tiempo.
es una cierta función del tiempo.
Como vemos, el tiempo no aparece explícitamente en la expresiones que dan las coordenadas de P.
5.5.1.4.- Configuración de un sistema de partículas en el caso de vínculos móviles (sistema reónomo).
Cuando los vínculos cambian su forma, o su posición en función del tiempo (sistema reónomo), en la función [5.1.1.01], que da el vector posición de la partícula, o en las ecuaciones de transformación [5.1.1.02], aparecerá explícitamente el tiempo. Para que ello ocurra, es necesario que la ley que da la variación de la forma, o posición del vínculo, sea un dato. Veamos un ejemplo en la figura F5-5.5.1.8:
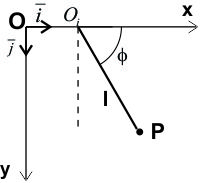
Figura F5-5.5.1.8
El punto de suspensión del péndulo se mueve de acuerdo con:
|
[5.1.1.03]
|
La posición de la partícula P considerada queda determinada con una única coordenada ![]() , ya que la posición de Oi está predeterminada por la [5.1.1.03].
, ya que la posición de Oi está predeterminada por la [5.1.1.03].
La coordenada vectorial de posición de la partícula P será:
|
[5.1.1.04]
|
o bien:
|
[5.1.1.05]
|
Como vemos, se trata de un sistema reónomo y en la [5.1.1.04] y [5.1.1.05] aparece explícitamente el tiempo, cosa que no ocurre cuando los vínculos no se mueven. El único parámetro independiente es ![]() .
.
También podríamos haber expresado la posición de P con vínculos superabundantes:
|
|
Con la siguiente ecuación de ligadura:
|
[5.1.1.06]
|
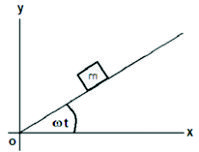
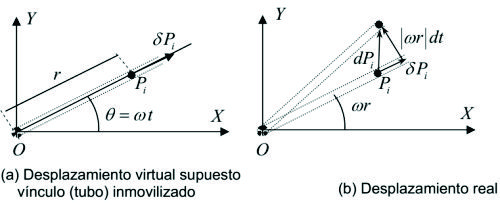
Otro ejemplo que podemos citar es el siguiente: supongamos una partícula que se mueve dentro de un tubo (vínculo móvil), el cual gira en un plano horizontal con velocidad angular ![]() constante y cuyo valor es un dato del problema. La posición de la partícula se configura con un único parámetro, que es la distancia de la partícula al eje de rotación, a la que llamaremos x. Las coordenadas de la partícula en un sistema fijo X, Y serán:
constante y cuyo valor es un dato del problema. La posición de la partícula se configura con un único parámetro, que es la distancia de la partícula al eje de rotación, a la que llamaremos x. Las coordenadas de la partícula en un sistema fijo X, Y serán:
|
[5.1.1.07]
|
En la [5.1.1.07], además del parámetro x, aparece explícitamente el tiempo.
En forma general, entonces, podemos expresar finalmente la configuración de un sistema de partículas en dónde los vínculos dependen del tiempo,como:
|
[5.1.1.08]
|
en donde los qk son parámetros independientes entre sí.
Las ecuaciones de transformación, tomarán finalmente la forma mas general:
|
[5.1.1.09]
|
5.5.1.5.- Desplazamiento real y desplazamiento virtual de las partículas de un sistema. Variación isocrónica de las coordenadas.
a).- Introducción.
Para expresar las definiciones referentes a esta cuestión, lo haremos a través de un ejemplo.
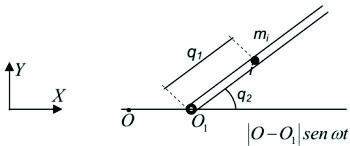
Consideremos el sistema, formado por una partícula i que se mueve dentro de un tubo liso. Cabe observar al respecto lo siguiente: hasta aquí hemos hablado de un sistema como un conjunto de N partículas i, lo que permite presentar los conceptos con la mayor generalidad posible. Pero en lo sucesivo, haremos extensiva la definición de sistema a lo que llamaremos un conjunto de elementos, los cuales pueden ser partículas propiamente dichas, o también barras, discos u otros cuerpos rígidos. En el ejemplo que consideraremos, los elementos del sistema son el tubo liso y la partícula i. En realidad, podemos considerar al tubo como un conjunto rígido de partículas, cuyo movimiento podemos referirlo a su centro de masa G.
Figura F5-5.5.1.9
El tubo puede girar en un plano vertical, alrededor de la articulación O1, como se muestra en la figura F5-5.5.1.9. A su vez la articulación O1, que es la ligadura que vincula al sistema con el exterior, se mueve con una ley conocida en función del tiempo. Si
es el módulo del vector posición O1, suponemos que dicha ley es:
La condición de vínculo establece que las partículas del tubo se mueven en trayectorias circulares alrededor de O1 y que las mismas no están fijas, sino que se trasladan a derecha e izquierda con un movimiento alternativo. A su vez la partícula i se mueve igual que las partículas del tubo (movimiento de arrastre) y además tiene un movimiento relativo de deslizamiento sobre el mismo.
De acuerdo con las consideraciones precedentes, se trata de un sistema reónomo (del griego rhéos, corriente y nomos, ley). Si O1 permaneciese fijo, el sistema tubo-partícula, sería esclerónomo (del griego sklerós, duro rígido y de nomos, ley).
Indicaremos ahora con Pi al vector posición de la partícula i(es decir, el vector que va desde O hasta Pi) referido a un sistema inercial (o “fijo”) XY.
Los parámetros de configuración son: la distancia de la partícula al punto O1, que la indicamos con q1 y el ángulo que forma el tubo con el eje X, que lo indicamos con q2.
Las ecuaciones de transformación, que dan las coordenadas de la partícula i en el sistema, XY, en función de los parámetros independientes q1, q2 y de
son:
Como
, resulta que dicho vector es una función de las coordenadas generalizadas y del tiempo:
Hemos usado el término coordenadas generalizadas, para indicar los parámetros independientes, tal como se definirá mas adelante. El tiempo aparece en forma explícita.
Por su parte las ecuaciones de transformación que dan las coordenadas del centro de masas G del tubo son:
O bien en forma vectorial:
Para definir el significado de desplazamiento virtual y establecer su diferencia con desplazamiento real (cuando la hay), que haremos en los párrafos siguientes centraremos nuestra atención en la partícula i ya que las definiciones serán igualmente válidas para el tubo G.
Hacemos el siguiente resumen de este caso:
Cantidad de partículas: 2, que son la partícula “i” y la “partícula” (por así llamarla), G.
Cantidad de parámetros independientes: 2 (hemos tomado q1 y q2).
Cantidad de ecuaciones de transformación: 4 ecuaciones, dadas por (a) y (c), (2 ecuaciones por cada partícula)
Vínculo: la articulación “O1”. Vincula al conjunto tubo-partícula con el exterior.
Sistema reónomo: lo es porque el vínculo “O1”, se mueve con una ley conocida.
Usaremos el ejemplo de esta introducción, para explicar los conceptos de variación isocrónica de coordenadas, desplazamiento virtual y su diferencia con desplazamiento real, en el artículo siguiente.
b).- Desplazamiento real, variación isocrónica de coordenadas y desplazamiento virtual.
Calcularemos a continuación el desplazamiento que experimenta la partícula i cuando transcurre un tiempo dt. Dicho desplazamiento, lo podemos expresar como el diferencial de la función vectorial Pi, dado por la expresión “(b)”. Dicho diferencial, lo se obtiene como la suma de los 3 diferenciales parciales con respecto a cada variable:
dPi es el vector desplazamiento “real” de la partícula i.
Si llamamos qk a una coordenada genérica, en un sistema de partículas con h coordenadas generalizadas, y si tenemos en cuenta la [5.1.1.08] (de parámetros de configuración) podemos escribir, en general:
Imaginaremos ahora que es posible que pueda variar una sola coordenada, por ejemplo el ángulo q2, sin que cambie q1 y sin que varíe la distancia
.
No hay inconveniente en imaginar que pueda variar un solo parámetro, en este caso q2, sin que cambien los otros q1..... qk, porque dichos parámetros pueden variar en forma independiente entre sí. Pero no es posible, en cambio, que varíe q2 sin que se mueva el vínculo (articulación) O1.
Para imaginar que cambia q2 sin que se mueva el vínculo, será necesario suponer, arbitrariamente, que el tiempo se “inmoviliza” o “no transcurre” solamente para el vínculo, mientras que si transcurre mientras cambia q2.
Supongamos, entonces, que la coordenada q2 experimenta una variación, mientras el vínculo permanece “inmovilizado” en la posición que ocupaba en un determinado instante t = t1 ó t = t2. Ello equivale a imaginar que en t = t1t, el vínculo (en este caso la articulación O1) “se detiene”, durante el tiempo que dura la variación de la coordenada q2. Llamaremos “isocrónica” a esa variación y la indicaremos con
. El término isocrónico se refiere a la suposición ya expresada, que el vínculo queda transitoriamente inmovilizado en la posición que ocupaba en un determinado instante t = t1, mientras dura la variación de las qk.
Para indicar el desplazamiento de Pi producido por la variación isocrónica de una coordenada, también se usa el símbolo
. Se ha usado en lugar del símbolo “d” de diferencial para indicar que no se trata del desplazamiento real, sino de un desplazamiento virtual o “imaginado”.
Al ocurrir la variación isocrónica
, la partícula Pi sufrirá un desplazamiento que se indica con el vector
en la figura F5-5.5.1.10 (a). Llamaremos al mismo desplazamiento virtual parcial debido a
.
Figura F5-5.5.1.10
Si imaginamos ahora que ocurre una variación isocrónica
de la coordenada q1 la partícula i experimentará un vector desplazamiento virtual
que se muestra en la figura F5-5.5.1.10(b). Entonces, podemos expresar los desplazamientos virtuales parciales de la partícula i, de la siguiente forma:
Si extendemos las consideraciones de este ejemplo a un sistema de N partículas i con h parámetros independientes de configuración y llamamos qk a un parámetro de orden k, podemos escribir:
es el desplazamiento virtual parcial de la partícula i, debido a la variación isocrónica
del parámetro qk. Finalmente si queremos obtener el desplazamiento virtual
, correspondiente a una variación isocrónica simultánea de los h parámetros independientes, debemos sumar los desplazamientos virtuales parciales correspondientes a cada una de ellas. Por lo tanto, podemos escribir:
En la figura F5-5.5.1.11 se muestra el vector desplazamiento virtual
. Debe observarse que si los vínculos son fijos (no dependen del tiempo, sistema esclerónomo), el último término de la (1) desaparece y el vector desplazamiento real de las partículas del sistema es coincidente con el vector desplazamiento virtual.
Figura F5-5.5.1.11
Podemos establecer el siguiente resumen con respecto a las características salientes del desplazamiento virtual de una partícula i del sistema:
Suponiendo el vínculo fijo, dicho desplazamiento debe ser compatible con la condición de vínculo, es decir moverse según la tangente a la trayectoria que le impone dicha condición.
Si los vínculos son móviles , se consideran inmovilizados los vínculos mientras dura la variación de las qk.
En el caso que los vínculos sean fijos, no se establece diferencias entre el vector desplazamiento real dPi y el vector desplazamiento virtual
de cada partícula. Tal sería el caso que el vínculo fuese realmente fijo en la figura F5-5.5.1.11.
El desplazamiento virtual no necesariamente debe ser un valor diferencial: puede ser un valor finito, siempre cuando los desplazamientos de las partículas del sistema, sean compatibles con los vínculos.
El símbolo
usado para indicar un desplazamiento virtual, cuando éste es una magnitud diferencial, participa de las mismas propiedades usuales del símbolo d usado como diferencial.
Un desplazamiento virtual puede ser un desplazamiento de un punto, como tal, pero también puede corresponder a la variación de un ángulo. O sea que puede medirse en metros o en radianes.
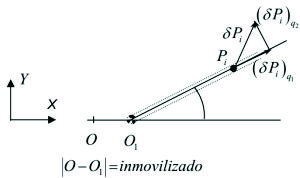
En la figura F5-5.5.1.12 se muestra otro ejemplo: se trata de un tubo que gira en un plano horizontal liso, articulado en un punto “O” fijo.
Figura F5-5.5.1.12
El sistema tiene un solo grado de libertad, correspondiente a la coordenada r. El ángulo
no es una coordenada generalizada porque varía con una ley dada,
.
En la figura F5-5.5.1.12(a) se muestra el vector desplazamiento virtual de la partícula Pi.
En F5-5.5.1.12(b) se indica el desplazamiento real dPi que tiene en cuenta el movimiento del vínculo. Al vector desplazamiento
debe agregarse un vector desplazamiento transversal producido por el movimiento del vínculo(en este caso el tubo)y cuyo módulo vale
.
Es de interés observar que en el desplazamiento virtual
,la reacción de vínculo no realiza trabajo. En cambio en el desplazamiento real dPi el trabajo de la fuerza de ligadura es diferente a cero.
5.5.1.6 Grados de libertad.
Se llaman grados de libertad a cada uno de los desplazamientos virtuales, independientes entre sí, que pueden tener las partículas de un sistema.
Supongamos un sistema de N partículas materiales, tal que su configuración está dada por n parámetros de Lagrange. qj con j = 1,2,3......n. El sistema está sometido a m ecuaciones de restricción de vínculo, o también puede no tener vínculos. Esta definición de grados de libertad es válida independientemente de la forma que tengan las ecuaciones de vinculo, es decir, ya sean estas ecuaciones finitas o diferenciales, integrables o no.
Entonces, si llamamos h a la cantidad de grados de libertad de un sistema, ésta queda dada por:
h = n - m |
5.5.2.- Coordenadas generalizadas o parámetros de configuración o coordenadas de Lagrange.
5.5.2.1.- Definición.
A los parámetros qk independientes entre sí, que determinan la configuración instantánea de un sistema ya mencionados, es usual y resulta cómodo, darles el nombre de coordenadas generalizadas.
En los sistemas holónomos, como ya se dijo, la cantidad de coordenadas generalizadas coincide con la cantidad de grados de libertad h del sistema. En consecuencia podemos expresar las ecuaciones de transformación que dan las coordenadas cartesianas de las N partículas, en función de las h coordenadas generalizadas qk, de la siguiente forma:
|
[5.5.2.01]
|
En las ecuaciones [5.5.2.01] aparece el tiempo en forma explícita, porque se considera el caso general de vínculos móviles.
Algunos ejemplos de coordenadas generalizadas:
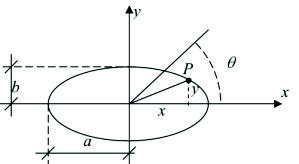
a) Partícula que se mueve sobre vínculo con forma de elipse.
Figura F5-5.5.2.01
La partícula tiene un solo grado de libertad. Tomamos como coordenada generalizada el ángulo
, (figura F5-5.5.2.01). Las ecuaciones de transformación, resultan las siguientes:
b) Cilindro que rueda sobre un plano inclinado.
Figura F5-5.5.2.02
Si la rodadura se hace sin deslizamiento se tiene una sola coordenada generalizada, que puede x(figura F5-5.5.2.02). El ángulo
se relaciona con x mediante la relación:
En cambio si hay deslizamiento en el punto de contacto, el sistema tiene 2 grados de libertad y las coordenadas generalizadas son x y
.
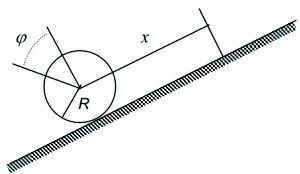
c) Barra articulada con cuerpo, sujeto a un resorte deslizante sobre él (figura F5-5.5.2.03).
Figura F5-5.5.2.03
La barra puede girar en plano vertical alrededor de la articulación O1.“a” es una determinada longitud del resorte, a partir de la cual medimos las elongaciones x del cuerpo.
En la tabla siguiente, se analizan diversas alternativas que pueden presentarse.
Situación
Coordenadas generalizadas
Ecuaciones de transformación
Vinculo
O1 Fijo.
, x
XP = XP(x,
)
YP = YP(x,
)
Esclerónomo
O1 Fijo,
varía con una ley conocida:
=
.
x
XP = XP(x, t)
YP = YP(x, t)
Reónomo
Distancia
y
siguen una ley conocida:
y
=
.
x
XP = XP(x, t)
YP = YP(x, t)
Reónomo
O1 se puede mover sobre una colisa deslizante y
sigue una ley conocida:
=
, x
XP = XP(x,
, t)
YP = YP(x,
, t)
Reónomo
Solo la distancia
sigue una ley conocida.
, x
XP = XP(x,
, t)
YP = YP(x,
, t)
Reónomo
Ninguno de los parámetros obedece a una ley predeterminada.
, x,
XP = XP(x,
,
)
YP = YP(x,
,
)
Esclerónomo
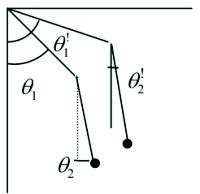
d) Péndulo doble (figura F5-5.5.2.04).
Las coordenadas generalizadas son
y
.
puede variar independientemente de
. (y además
puede variar independientemente de
), tal como se puede observar en el dibujo.
Figura F5-5.5.2.04
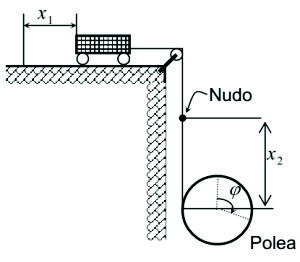
e) En la figura F5-5.5.2.05 un extremo de la cuerda está atado a un bloque que desliza sobre un plano horizontal. En el otro extremo se encuentra enrollada sobre una polea, que al caer, se va desenrollando.
Las coordenadas generalizadas pueden ser: x1 y x2, o también x1 y
Figura F5-5.5.2.05
5.5.3.- Trabajo virtual y fuerza generalizada de orden k.
Para establecer las definiciones de trabajo virtual y fuerza generalizada de orden k, lo haremos a partir de un ejemplo en particular, que se muestra en la figura F5-5.5.3.01, para luego darle validez general. En la mencionada figura, se indica el sistema formado por el tubo liso de largo l articulado en O1 y la partícula i, de masa mi. La partícula puede deslizar a lo largo del tubo.
En la figura F5-5.5.3.01 se ven las coordenadas generalizadas, queson q1 (distancia) y q2 (ángulo).
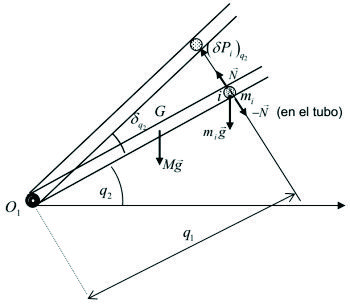
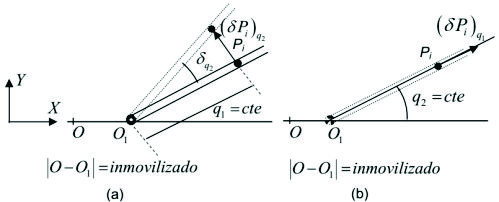
Figura F5-5.5.3.01: variación de q2, suponiendo que q1 permanece constante
En el análisis que haremos seguidamente será indistinto que el vínculo O1 se mueva, o no, porque consideraremos variaciones isócrónicas de las coordenadas y desplazamientos virtuales de las partículas.
Llamaremos trabajo virtual de orden k (o trabajo virtual asociado a la coordenada qk) al trabajo de las fuerzas que actúan en todas las partículas del sistema, cuando las mismas experimentan un desplazamiento virtual parcial de orden k, es decir, un desplazamiento debido a la variación isócrona (o virtual) de una coordenada qk. Indicaremos con ![]() o con
o con ![]() a este trabajo virtual de orden k.
a este trabajo virtual de orden k.
Al referirnos a las fuerzas que actúan en todas las partículas del sistema, incluimos a las fuerzas activas y (al menos en teoría) a las fuerzas de vínculos o ligaduras. Pero como comprobaremos en este artículo, el trabajo de estas últimas siempre resulta nulo y en consecuencia, el trabajo virtual puede calcularse como sólo el trabajo de las fuerzas activas del sistema, excluyendo el trabajo de las fuerzas de ligadura.
Referido al ejemplo de la figura F5-5.5.3.01, comenzaremos calculando el trabajo ![]() correspondiente a una variación
correspondiente a una variación ![]() . Suponemos que q1 permanece constante al variar q2.
. Suponemos que q1 permanece constante al variar q2.
Al ocurrir una variación ![]() , el centro de masas G del tubo, se mueve sobre un arco de radio l/2 y la partícula i se mueve sobre un arco de radio q1 = cte. Las fuerzas actuantes en los elementos del sistema son:
, el centro de masas G del tubo, se mueve sobre un arco de radio l/2 y la partícula i se mueve sobre un arco de radio q1 = cte. Las fuerzas actuantes en los elementos del sistema son:
La reacción de vínculo en la articulación O1, que la llamaremos
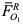 (no se la dibujó en la figura F5-5.5.3.01)
(no se la dibujó en la figura F5-5.5.3.01)El peso del tubo
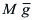
El peso de la partícula
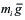
El par acción-reacción
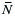 y -
y -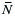 que son las fuerzas de ligadura internas entre la partícula y el tubo. Tienen dirección normal a este último.
que son las fuerzas de ligadura internas entre la partícula y el tubo. Tienen dirección normal a este último.
Podemos expresar entonces, el trabajo virtual ![]() , como la suma de los siguientes productos escalares:
, como la suma de los siguientes productos escalares:
|
(1)
|
Observamos ahora algo que tendrá mucha importancia mas adelante y sobre lo cual volveremos: si damos un desplazamiento isocrónico ![]() , el trabajo virtual de las fuerza actuantes en el sistema se calcula usando sólo las fuerzas activas (en este caso
, el trabajo virtual de las fuerza actuantes en el sistema se calcula usando sólo las fuerzas activas (en este caso ![]() y
y ![]() ), porque las fuerzas reactivas no realizan trabajo. Podemos expresar entonces la (1) en forma más general como:
), porque las fuerzas reactivas no realizan trabajo. Podemos expresar entonces la (1) en forma más general como:
|
|
En donde ![]() es la fuerza activa que actúa en cada partícula del sistema.
es la fuerza activa que actúa en cada partícula del sistema.
Calculemos ahora el trabajo virtual asociado a la variación de q1, que es ![]() (figura F5-5.5.3.01)
(figura F5-5.5.3.01)
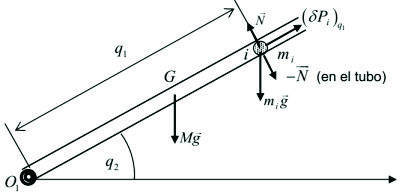
Figura F5-5.5.3.02: Variación de q1, suponiendo que q2 permanece constante
|
|
El trabajo que hace la fuerza de ligadura interna ![]() vale cero, por ser
vale cero, por ser ![]() perpendicular a
perpendicular a ![]() (vínculo liso).
(vínculo liso).
|
|
entonces,
|
(2)
|
y en forma más general, para el caso de N partículas:
|
|
Como vemos al variar sólo q1, tampoco intervienen las fuerzas de vínculo liso. En caso de haber fuerzas de rozamiento con el tubo, dicha fuerza puede incluirse dentro de las fuerzas activas y considerar la reacción de vínculo normal al tubo.
La no aparición de las fuerzas de vínculo en la expresión del trabajo virtual de un sistema, que se puso de manifiesto en este ejemplo, tiene validez general.
Si llamamos ahora ![]() al trabajo virtual que se realiza en un sistema de N partículas Pi, cuando una sola coordenada qk experimenta un desplazamiento isócrono
al trabajo virtual que se realiza en un sistema de N partículas Pi, cuando una sola coordenada qk experimenta un desplazamiento isócrono ![]() , podemos escribir:
, podemos escribir:
|
(3)
|
pero, como el vector P es una función de las coordenadas generalizadas, que se expresa como: P1 = P1(q1,q2,...,qk,...,qh,), resulta:
|
(4)
|
reemplazamos (4) en (3):
|
(5)
|
El primer miembro de la (5) es, como se dijo, el trabajo virtual de la totalidad de las fuerzas activas cuando una sola coordenada varía en ![]() (con vínculos quietos). En el segundo miembro, aparece la variación
(con vínculos quietos). En el segundo miembro, aparece la variación ![]() que multiplica al factor
que multiplica al factor  , al que llamaremos fuerza generalizada de orden k y lo indicaremos con Qk.
, al que llamaremos fuerza generalizada de orden k y lo indicaremos con Qk.
Entonces:
|
(6)
|
h es la cantidad de coordenadas generalizadas, que coincide con la cantidad de grados de libertad (sistema holónomo).
Debe observarse que, de acuerdo con la (6), la fuerza generalizada es una magnitud escalar, porque cada término de la sumatoria es un producto escalar del vector ![]() por el vector
por el vector ![]() .
. ![]() es la resultante de las fuerzas activas que obran sobre cada partículas. Como surge de la (6), las
fuerzas de ligadura no intervienen en el cálculo de la fuerza generalizada.
es la resultante de las fuerzas activas que obran sobre cada partículas. Como surge de la (6), las
fuerzas de ligadura no intervienen en el cálculo de la fuerza generalizada.
En base a las consideraciones precedentes, podemos escribir el trabajo virtual de orden k, dado por la (5), de la siguiente forma,
|
(7)
|
donde la fuerza generalizada Qk viene dada por la (6).
Es importante tener presente que las unidades de qk y de ![]() pueden corresponder a un ángulo o a un desplazamiento y por lo tanto se pueden medir en radianes o metros. Por lo tanto, las unidades de Qk podrán ser tanto Nm (si
pueden corresponder a un ángulo o a un desplazamiento y por lo tanto se pueden medir en radianes o metros. Por lo tanto, las unidades de Qk podrán ser tanto Nm (si ![]() está en radianes) o N (si
está en radianes) o N (si ![]() está en metros).
está en metros).
5.5.3.1.- Procedimiento para calcular la fuerza generalizada de orden k, resumen.
A continuación se reseña el procedimiento para calcular la fuerza generalizada de orden k en un sistema:
Hacemos variar una sola coordenada y calculamos el trabajo que hacen las fuerzas activas del sistema. Si hubiese vínculos móviles, éstos deben considerarse inmovilizados, para que el desplazamiento sea virtual. Si en las ligaduras hubiese fuerzas por deslizamiento, éstas deben incluirse junto con las fuerzas activas, de manera que los vínculos pueden asimilarse a vínculos lisos.
Expresamos la suma de trabajos de las fuerzas activas en cada partícula o elemento del sistema, como el producto de dos factores: uno de ellos, deberá ser
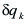 y entonces, el otro factor será la fuerza generalizada de orden k Qk quebuscamos, como se indica en la (7).
y entonces, el otro factor será la fuerza generalizada de orden k Qk quebuscamos, como se indica en la (7).Por último, si quisiéramos expresar el trabajo virtual que hacen las fuerzas del sistema cuando ocurre una variación isócrona simultánea de las h coordenadas generalizadas deberemos escribir:
 (8)
(8)donde el vector
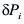 , de acuerdo con la (5) (de desplazamiento virtual), se expresa como:
, de acuerdo con la (5) (de desplazamiento virtual), se expresa como: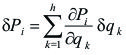
y, por lo tanto, el trabajo virtual por variación simultánea de todas las coordenadas es:
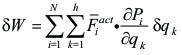 (9)
(9)
5.5.3.2.- Ejemplos de cálculo de las fuerzas generalizadas.
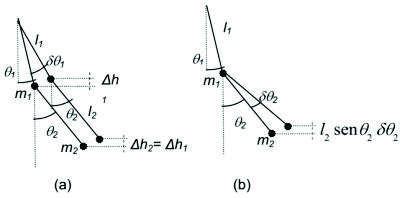
a) Cálculo de las fuerzas generalizadas en el péndulo doble: (figura F5-5.5.3.03).
Figura F5-5.5.3.03
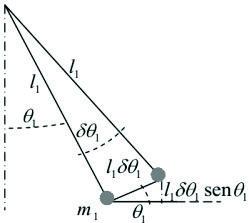
Variación de
((
permanece constante, figura F5-5.5.3.03a): para una mejor comprensión ampliamos parte del dibujo en la figura F5-5.5.3.04.
Figura F5-5.5.3.04
Variación de (
(
permanece constante, figura F5-5.5.3.03b):
La expresión precedente, nos permite expresar una definición práctica del concepto de fuerza generalizada, de la siguiente manera:
Observamos que al dar un desplazamiento
a una de las coordenadas generalizadas, las fuerzas obrantes sobre el sistema realizan un trabajo que es
y que ese trabajo elemental queda expresado mediante dos factores: Qk y
.
Entonces decimos que, la fuerza generalizada asociada a una coordenada generalizada, es el factor que multiplica al desplazamiento de dicha coordenada generalizada, en la expresión del trabajo del sistema correspondiente, a una variación elemental de esa coordenada.
b) Calculo de las fuerzas generalizadas en el siguiente sistema:
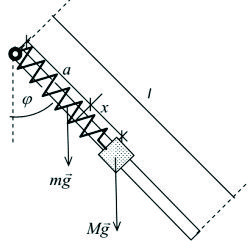
Una masa M, articulada a un resorte se desliza sobre una varilla de masa m y longitud l. La varilla puede girar en el plano vertical barriendo el ángulo
.(figura F5-5.5.3.05)
Llamaremos:
: longitud del resorte en equilibrio para un cierto valor de
inicial.
x: desplazamiento longitudinal, medido desde
.
Figura F5-5.5.3.05
Calculo de la fuerza generalizada para la coordenada
. (para este cálculo, suponemos que x permanece constante):
La expresión que multiplica a
, es la fuerza generalizada correspondiente a
y resulta:
Calculo de la fuerza generalizada para la coordenada x.(para este cálculo, suponemos que
permanece constante):
5.5.3.3.- Principio de los trabajos Virtuales, ecuación simbólica de la estática.
El principio de los trabajos virtuales se enuncia de la siguiente forma:
En un sistema de partículas con vínculos bilaterales (aquellos en que el punto está permanentemente en contacto con el vínculo), si las fuerzas actuantes están en equilibrio, el trabajo virtual de mismas es cero.
De acuerdo con la enunciación de este principio, podemos escribir:
|
|
o bien, deacuerdo con la (8) (de trabajo virtual):
|
(1)
|
donde ![]() es el desplazamiento de cada partícula cuando ocurre una variación simultánea de todas las coordenadas generalizadas.
es el desplazamiento de cada partícula cuando ocurre una variación simultánea de todas las coordenadas generalizadas.
5.5.4.- Ecuación simbólica de la Dinámica o Principio de D'Alambert.
Teniendo en cuenta la segunda Ley de Newton:
|
|
|
Por el principio de trabajo virtuales:
|
|
|
Donde:
![]() Cantidad de movimiento lineal (cambiamos el símbolo de L para no confundir con el Lagrangiano, que posteriormente veremos)
Cantidad de movimiento lineal (cambiamos el símbolo de L para no confundir con el Lagrangiano, que posteriormente veremos)
![]() Fuerza activa conocida.
Fuerza activa conocida.
![]() Fuerza debida a la ligadura.
Fuerza debida a la ligadura.
|
|
[5.5.4.01]
|
Es importante recalcar sobre la expresión anterior que:
No aparecen las fuerzas de ligadura.
Tenemos una ecuación Dinámica.
5.5.5.- Ecuación de Lagrange para un sistema Holonómico.
Se formulan las ecuaciones del movimiento en términos de las coordenadas generalizadas. Se tiene que:
Se reduce el número de ecuaciones a resolver.
" No aparecen las reacciones a resolver.
5.5.5.1.- Introducción a las ecuaciones de Lagrange.
Considerando el movimiento de una partícula en un plano bajo la acción de una fuerza ![]() . Escribimos la ecuación de Newton en coordenadas polares:
. Escribimos la ecuación de Newton en coordenadas polares:
|
|
|
|
|
|
Queremos construir una formulación energética, en el sentido de que podamos partir de la energía cinética:
|
|
|
y llegar a las ecuaciones de Newton, por medio de algún operador D tal que, por ejemplo ![]() . Notablemente este no es una tarea complicada. Trabajando un poco dicho término:
. Notablemente este no es una tarea complicada. Trabajando un poco dicho término:
|
|
|
Podemos escribir la componente radial de la ecuación de Newton en términos de la energía cinética:
|
|
|
Podemos escribir ambas como una sola, en términos de la coordenada ![]() :
:
|
|
[5.5.5.01]
|
Esta es la ecuación de Lagrange. La demostración es completamente correcta, pero deja en duda un aspecto muy importante, se realizó la deducción para una sola partícula, donde la fuerza incluye "todas" las interacciones que actúan sobre ella, incluidas las fuerzas de vínculo o ligaduras, pero con el principio de D'Alambert se eliminó estas últimas para un sistema, por lo que mejor sería la deducción de las ecuaciones de Lagrange a partir del Principio de D'Alambert, demostrando que aquella vale para todo el sistema (no sólo una partícula) y para cualquier coordenadas generalizadas q compatibles con los grados de libertad del sistema.
5.5.5.2.- Ecuaciones de Lagrange.
Trabajando sobre la ecuación de D'Alambert para un sistema arbitrario de n partículas:
|
|
|
Los sumandos de la ecuación no son independientes, por lo que la ecuación de D'Alambert lo escribiremos en términos de las 3n-k coordenadas generalizadas qi del sistema, en función de las cuales las antiguas coordenadas, están dadas por:
|
|
|
Nuestro objetivo es demostrar que, en términos de estas coordenadas generalizadas, que el principio de D'Alambert se puede escribir como:
|
|
[5.5.5.02]
|
Cuya demostración lo haremos en el acápite posterior. Si las ligaduras son holónomas, las coordenadas generalizadas qi son independientes y, por lo tanto es la única manera que se cumpla la ecuación de D'Alambert es que se anule cada coeficiente por separado.
Si la definición de fuerzas generalizadas es:
|
|
|
Entonces:
|
|
|
Supongamos ahora que algunas de las fuerzas aplicadas sobre el sistema derivan de una función potencial U, que es la energía potencial del sistema: ![]() , en dicho caso podemos escribir las fuerzas generalizadas:
, en dicho caso podemos escribir las fuerzas generalizadas:
|
|
|
Reemplazando en las ecuaciones anteriores, podemos incorporar el potencial en el primer término:
|
|
[5.5.5.03]
|
Como el potencial U solo depende de la posición, debe se independiente de las velocidades generalizadas ![]() . Por ello podemos incluir el potencial U en la derivada parcial respecto de
. Por ello podemos incluir el potencial U en la derivada parcial respecto de ![]() , obteniendo la ecuación de Lagrange:
, obteniendo la ecuación de Lagrange:
|
|
[5.5.5.04]
|
|
Donde hemos definido el Lagrangiano |
[5.5.5.05]
|
5.5.5.3.- Demostración de las ecuaciones de Lagrange.
Nos falta demostrar:
|
|
|
A partir del principio de D'Alambert (Sin anular las fuerzas de ligadura):
|
|
|
El trabajo virtual de las fuerzas generalizadas es:
|
|
(1)
|
También:
|
|
|
Ahora bien, por un lado tenemos que:
|
|
|
y por otro lado:
|
|
|
Reemplazando en la ecuación anterior:
|
|
|
|
|
(2)
|
Sumando (1) y (2) se tiene:
|
|
|
5.5.5.4.- Resumen de la ecuación de Lagrange.- La ecuación de Lagrange es muy útil para deducir ecuaciones de movimiento usando energías potenciales y cinéticas. Como para calcular esas energías se usan posiciones y velocidades, no se involucra ninguna aceleración y de esta manera la parte cinemática del problema se simplifica mucho. Usando un sistema adecuado de coordenadas adecuado, se pueden obtener las ecuaciones de movimiento de una manera sencilla y directa. A continuación se enlistan tres formas de la ecuación de Lagrange:
1.- La forma general es:
|
[1]
|
en donde:
|
[2]
|
2.- Para sistemas conservativos:
|
[3]
|
en donde:
|
[4]
|
3.- La forma alternativa global, es:
|
[5]
|
Finalmente, resumamos tres métodos para calcular las fuerzas generalizadas.
Notamos que en la deducción de la ecuación de Lagrange, la fuerza generalizada puede calcularse de acuerdo con:
|
[6]
|
Sin embargo, la fuerza generalizada también puede calcularse considerando el trabajo virtual realizado por la fuerza generalizada al actuar a través de un desplazamiento virtual generalizado, es decir, ![]() . Eso se ilustra en el ejemplo N° 2.
. Eso se ilustra en el ejemplo N° 2.
Un tercer método para calcular fuerzas generalizadas se aplica solamente a sistema de fuerzas conservativas y se usó al deducir la ecuación de Lagrange para un sistema conservativo; es decir:
|
[7]
|
Este método también se ilustrará mediante un ejemplo. En la práctica, la ecuación de Lagrange para un sistema conservativo se usa invariablemente, en lugar de la ecuación de Lagrange en forma general, con la ecuación anterior para fuerzas generalizadas.
5.5.5.5.- Ejemplos ilustrativos:
1.- Aplicación de las ecuaciones para fuerzas generalizadas. Calcular las fuerzas generalizada en coordenadas cilíndricas (r, ![]() , z), para una partícula sujeta a la acción de una fuerza F, aplicando las ecuaciones para fuerzas generalizadas.
, z), para una partícula sujeta a la acción de una fuerza F, aplicando las ecuaciones para fuerzas generalizadas.
Solución
Considerando que la fuerza está expresada como:
![]()
y la relación entre las coordenadas rectangulares (x, y, z) y cilíndricas (r, ![]() , z), es:
, z), es:
![]()
Aplicando las ecuaciones para las fuerzas generalizadas, tenemos:
![]()
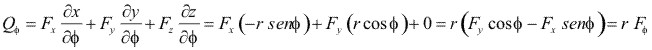
![]()
Luego: ![]()
2.- Calcular fuerzas generalizadas considerando el trabajo virtual. Calcular las fuerzas generalizadas en coordenadas cilíndricas (r, ![]() , z), para una partícula sujeta a la acción de una fuerza F, considerando el trabajo virtual realizado.
, z), para una partícula sujeta a la acción de una fuerza F, considerando el trabajo virtual realizado.
Solución
La fuerza F puede descomponerse en las componentes r, ![]() y z, que son Fr, F
y z, que son Fr, F![]() y Fz respectivamente. Designando las fuerzas generalizadas en las direcciones r,
y Fz respectivamente. Designando las fuerzas generalizadas en las direcciones r, ![]() y z, por Qr, Q
y z, por Qr, Q![]() y Qz, respectivamente y considerando el trabajo virtual realizado a través de los desplazamientos virtuales r,
y Qz, respectivamente y considerando el trabajo virtual realizado a través de los desplazamientos virtuales r, ![]() y z, tenemos:
y z, tenemos:
![]()
Por consiguiente las fuerzas generalizadas, son:
![]()
3.- Ecuación de lagrange - movimiento de una partícula en coordenadas cilíndricas. Usando la ecuación de Lagrange, deducir las ecuaciones de movimiento en coordenadas cilíndricas (r, ![]() , z), para una partícula de masa m sujeta a la acción de una fuerza F.
, z), para una partícula de masa m sujeta a la acción de una fuerza F.
Solución
Expresando las relaciones entre las coordenadas cartesianas (x, y, z) y cilíndricas(r, ![]() , z), como:
, z), como:
![]()
Las derivadas con respecto al tiempo son:
![]()
La energía cinética Ek de la partícula, es:
![]()
Ilustraremos la forma general de la ecuación de Lagrange:
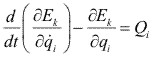
en donde ![]() . Las fuerzas generalizadas Qr, Q
. Las fuerzas generalizadas Qr, Q![]() y Qz ya han sido calculadas en los ejemplos anteriores.
y Qz ya han sido calculadas en los ejemplos anteriores.
Para la coordenada radial r, tenemos:
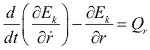
Donde: 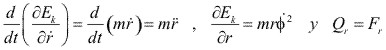 y la ecuación de movimiento es:
y la ecuación de movimiento es:
![]()
Para la coordenada transversal ![]() , tenemos:
, tenemos:
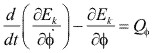
Donde: 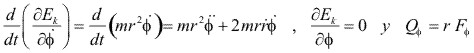 y la ecuación de movimiento es:
y la ecuación de movimiento es:
![]()
Para la coordenada axial z, tenemos:
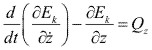
Donde: 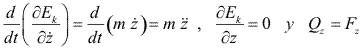 y la ecuación de movimiento es:
y la ecuación de movimiento es:
![]()
|
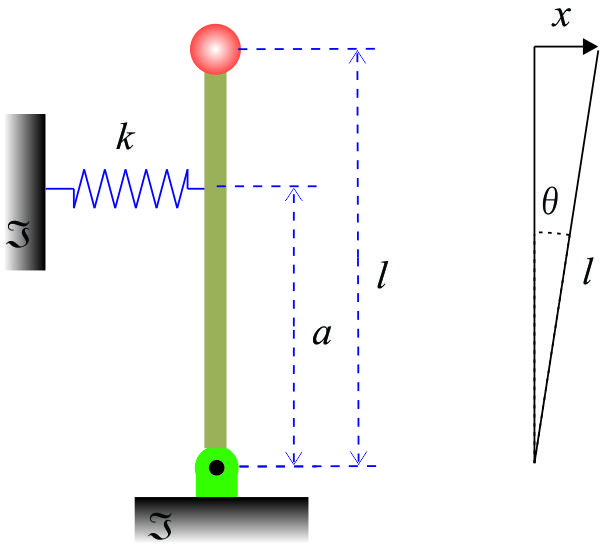
4.- Ecuación de Lagrange - vibración de una partícula. Deducir la ecuación de movimiento de un péndulo invertido que está restringido por un resorte cuya constante es k, como se indica en la figura. Se supone que la masa del péndulo está concentrada a una distancia l del punto de apoyo, y que el resorte es lo suficientemente rígido para que el péndulo sea estable. Úsese la ecuación de Lagrange.
|
|
Solución
Como el sistema es conservativo, se usará la ecuación correspondiente a sistemas conservativos (forma 2). Suponemos movimientos pequeños y usamos ![]() , para la masa m. Las energías potencial y cinética se calculan como,
, para la masa m. Las energías potencial y cinética se calculan como,
![]()
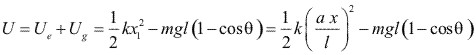
![]()
El Lagrangiano es:
![]()
Aplicando la ecuación de Lagrange:
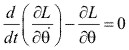
Con: 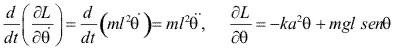 , obtenemos la ecuación de movimiento:
, obtenemos la ecuación de movimiento:
![]()
Haciendo lineal la ecuación de movimiento, al notar que, para ángulos pequeños ![]() , tenemos:
, tenemos:
![]()
o bien:
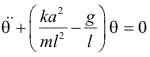
5.- Ecuación de Lagrange - vibración de una partícula. Deducir la ecuación del movimiento del ejemplo anterior, usando la forma general de la ecuación de Lagrange.
Solución
La ecuación de Lagrange, en la forma general, es:

A partir del ejemplo anterior, tenemos:
![]()
Por tanto, 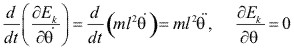 y la fuerza generalizada Q
y la fuerza generalizada Q![]() puede calcularse a partir de:
puede calcularse a partir de:
![]()
Por consiguiente, la ecuación de movimiento es:
![]()
|
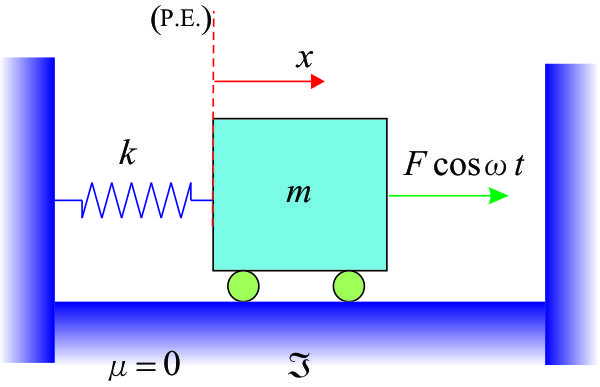
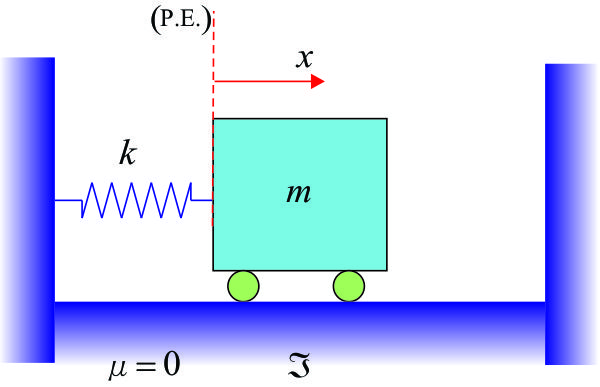
6.- Ecuación de Lagrange - vibración de una partícula. Deducir las ecuaciones de movimiento para las vibraciones libres y forzada de un sistema que tiene un grado de liberta y que consiste de una masa y un resorte (ver figura).
|
|
Solución
Usamos la ecuación de Lagrange en la forma:
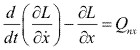
Las energías cinética y potencial, son:
![]()
y el Lagrangiano es:
![]()
La fuerza generalizada, no conservativa, es:
![]()
Aplicando la ecuación de Lagrange, con:

Obtenemos:
![]()
5.5.5.6.- Ejemplos ilustrativos, para sistema de partículas:
|
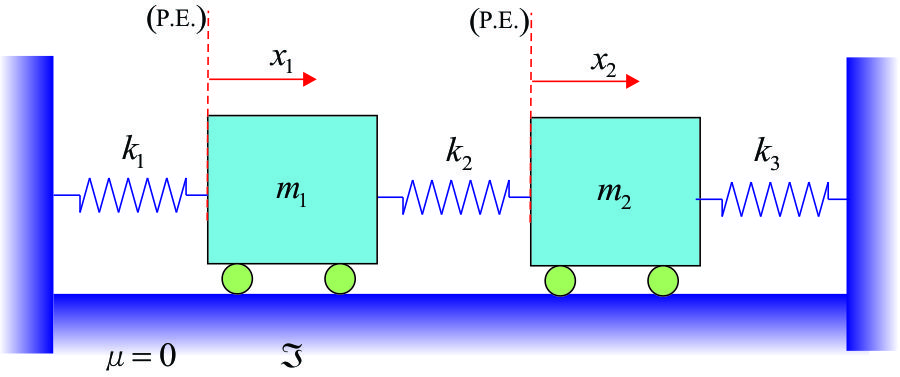
1.- Ecuación de Lagrange - dos partículas en vibración libre. Deducir las ecuaciones de movimiento para la vibración libre de un sistema que tiene dos grados de libertad, como se indica en la figura. |
|
Solución
Ya que el sistema es conservativo, usaremos la ecuación de Lagrange para el sistema conservativo:
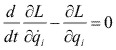
en donde: ![]()
Las energías cinética y potencial son:
![]()
![]()
y el Lagrangiano, es:
![]()
Para la coordenada x1, tenemos:
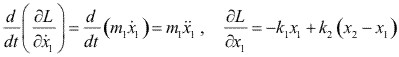
y la ecuación de movimiento, es:
![]()
Para la coordenada x2, tenemos:
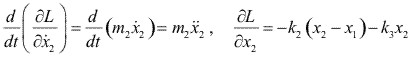
y la ecuación de movimiento, es:
![]()
|
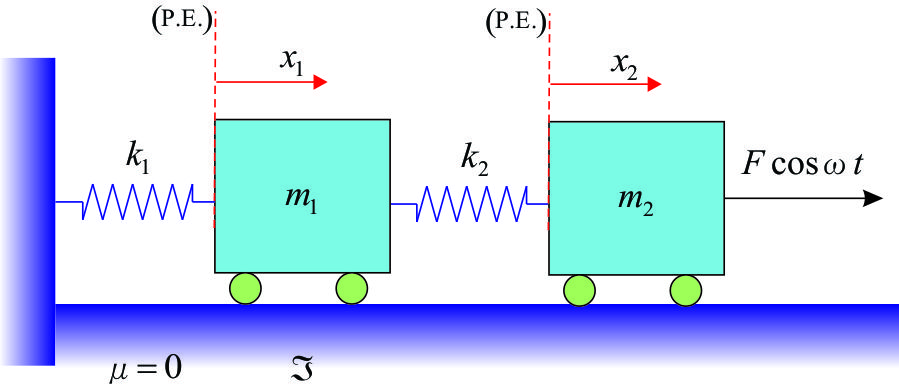
2.- Ecuación de Lagrange - dos partículas en vibración forzada. Deducir las ecuaciones de movimiento para la vibración forzada de un sistema que tiene dos grados de libertad, como se indica en la figura. |
|
Solución
Como la acción del sistema de fuerzas es parcialmente conservativo y parcialmente no conservativo, usaremos la ecuación de Lagrange en la forma:
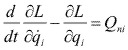
Las energías cinética y potencial, son:
![]()
y el Lagrangiano, es:
![]()
Para la coordenada x1, tenemos:

y la ecuación de movimiento, es:
![]()
Para la coordenada x2, tenemos:

y la ecuación de movimiento, es:
![]()
|
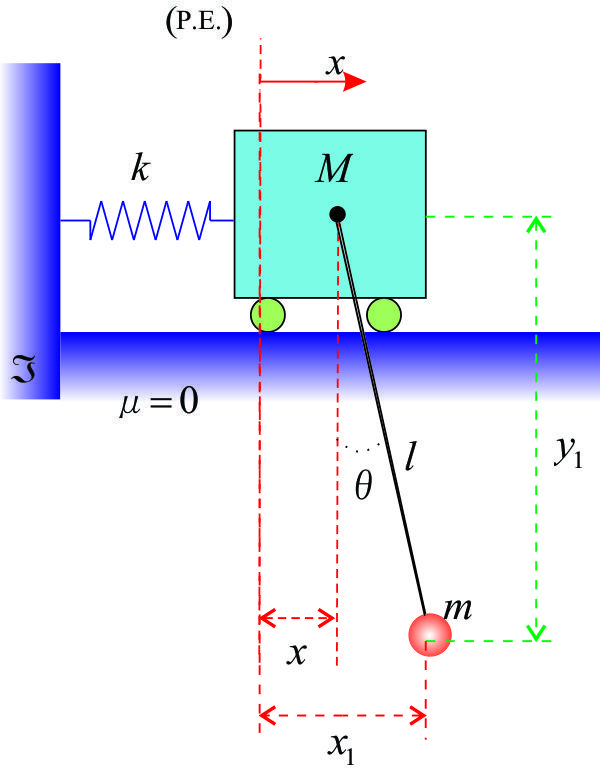
3.- Ecuación de Lagrange - dos partículas. Usando la ecuación de Lagrange, deducir las ecuaciones de movimiento para el sistema mostrado en la figura.
|
|
Solución
Tomando a x y ![]() como coordenadas generalizadas para el sistema, tenemos, para la partícula m,
como coordenadas generalizadas para el sistema, tenemos, para la partícula m, ![]() , Sea v la velocidad de la partícula. Entonces:
, Sea v la velocidad de la partícula. Entonces:
![]()
Las energías cinética y potencial, son:
![]()
![]()
![]()
y el Lagrangiano, es:
![]()
Para la coordenada x, tenemos:
![]()
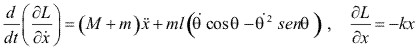
y la ecuación de movimiento, es:
![]()
Para la coordenada ![]() , tenemos:
, tenemos:
![]()
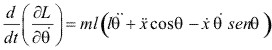
![]()
y la ecuación de movimiento, es:
![]()
4.- Ecuación de Lagrange - dos partículas. Usando la ecuación de Lagrange en la forma general, deducir las ecuaciones de movimiento para el sistema del ejemplo anterior. Calcular las fuerzas generalizadas de dos maneras; en términos de la energía potencial, y del trabajo virtual.
Solución
A partir del ejemplo anterior, tenemos:
![]()
![]()
Las fuerzas generalizadas pueden calcularse como:
![]()
![]()
A partir de la consideración del trabajo virtual, obtenemos:
![]()
![]()
|
El término
Para la coordenada x, tenemos:
|
|
y la ecuación de movimiento, es:
![]()
Para la coordenada ![]() , tenemos:
, tenemos:
![]()
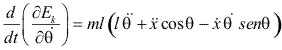
![]()
y la ecuación de movimiento, es:
![]()
Por su puesto, estas dos ecuaciones son iguales a las que se dedujeron en el ejemplo anterior.
- En la ecuación de Lagrange, existe una ecuación por cada grado de libertad, por lo que la elección de coordenadas generalizadas libres conduce directamente al mínimo número de ecuaciones dinámicas.
- Se trata de ecuaciones diferenciales de segundo orden (al existir derivadas temporales de los términos
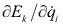 , que dependen, a su vez, de
, que dependen, a su vez, de 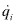 )
) - En las ecuaciones de Lagrange han quedado eliminadas todas las reacciones de enlace que no realizan trabajo virtual, correspondiente a los enlaces lisos. Esto contrasta con las ecuaciones procedente de los teoremas Newtonianos en las que, en principio, deben considerarse estas reacciones.
- Una vez evaluadas las expresiones de Ek y de Qi, las ecuaciones de Lagrange se pueden obtener de forma automática sin más que aplicar las reglas análiticas de derivación correspondiente a la ecuación.
- El significado físico del término
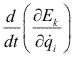 es de las fuerzas de inercia.
es de las fuerzas de inercia. - Por último, los términos
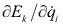 pueden interpretarse como fuerzas ficticias procedentes de la elección de coordenadas generalizadas
pueden interpretarse como fuerzas ficticias procedentes de la elección de coordenadas generalizadas 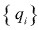 . En caso de que éstas sean simplemente las componentes cartesianas de los vectores
. En caso de que éstas sean simplemente las componentes cartesianas de los vectores 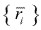 desaparecerían. Estas fuerzas se añaden a las fuerzas generalizadas Qi en la dirección de qi.
desaparecerían. Estas fuerzas se añaden a las fuerzas generalizadas Qi en la dirección de qi.
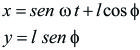
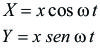
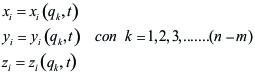
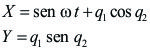
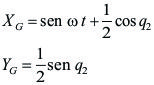
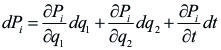
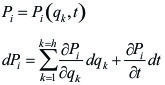
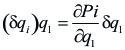
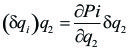
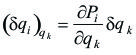
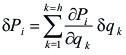
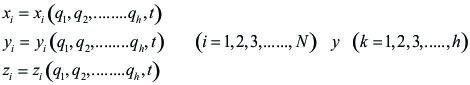
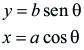
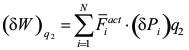
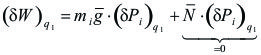
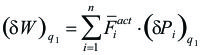
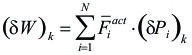
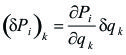
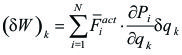

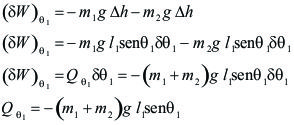
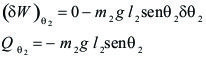
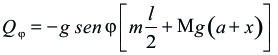
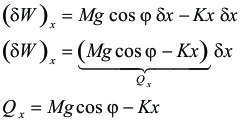
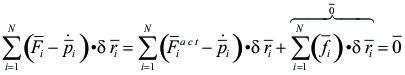 >
>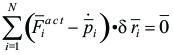 (Ecuación simbólica de la dinámica o Principio de D'Alambert)
(Ecuación simbólica de la dinámica o Principio de D'Alambert)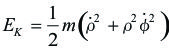
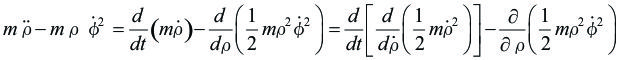
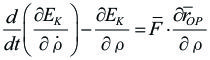
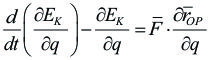

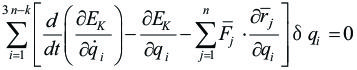
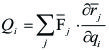
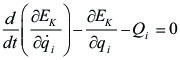
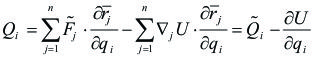
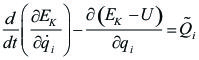
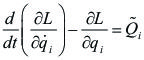
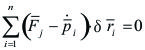
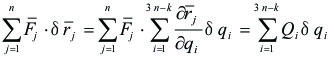
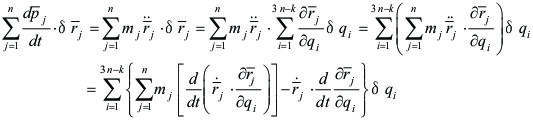
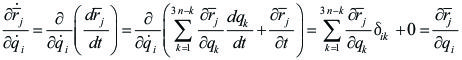
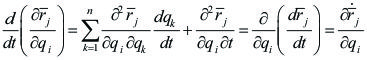

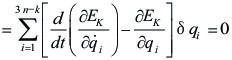
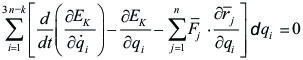 (Es igual a [5.5.5.02], por lo que quedo demostrado)
(Es igual a [5.5.5.02], por lo que quedo demostrado)