5.4.2.- Vibraciones forzadas amortiguadas.-

Ejemplo: Oscilador armónico simple forzado.

5.4.2.1.- Para fuerzas, o desplazamientos de base o cimentación armónicas:

i).- Si,

ii).- Si,

En donde, es la frecuencia o pulsación de la fuerza excitatriz o del desplazamiento, F₀ o K b amplitud de la fuerza excitatriz o del desplazamiento respectivamente.

Ecuaciones diferenciales no homogéneas de segundo orden y de coeficientes constantes, cuya solución está dado por:

a).- Para fuerzas del tipo armónico.-

La solución complementaria está dada por el caso subamortiguado:

ó

Determinando la solución particular de 5.4.2.1.0.1 de la forma:

Donde D y E son constantes que, no dependen de las condiciones iníciales, sino de la solución de la ecuación diferencial.

Derivando dos veces con respecto al tiempo la ecuación 5.4.2.1.0.3:

Reemplazando en 5.4.2.1.0.1 y agrupando:

Está ecuación es nula, siempre en cuando los coeficientes también sean nulas, luego:

Resolviendo 5.4.2.1.0.4, para D y de la misma manera para E, se tiene:

Escribiendo 5.4.2.1.0.3 en la forma:

Donde:

También:

Donde:

X₀ Amplitud de la solución particular, como esté es constante, a dicha solución se le da el nombre de vibración permanente.

Angulo de fase, representa el retraso de la respuesta , respecto a la fuerza aplicada . Es decir, la respuesta pasa por su máximo segundos después de que lo haga la fuerza aplicada.

F₀ Describe la deformación que produciría estáticamente al resorte y no tiene que ver nada con el equilibrio estático del sistema.

En 5.4.2.1.0.7 y 5.4.2.1.0.8 cuando C es pequeño toma valores próximo a la frecuencia natural , haciendo que la amplitud sea muy grande; y si C = 0 las frecuencias se hacen iguales y la amplitud se hace infinito, se dice que el sistema está en "resonancia".

Deformación estática o desplazamiento estático

La solución de la ecuación diferencial 5.4.2.1.0.1, es:

[5.4.2.1.0.9]

ó

En 5.4.2.1.0.10 las constantes de integración A₃ y A₄ deben calcularse a partir de las condiciones iniciales usando la respuesta total dada por la ecuación 5.4.2.1.0.10 y no sólo de la parte transitoria dado por la ecuación X_C. Examinando el componente transitorio de la respuesta, puede verse que la presencia del factor exponencial hará que este componente desaparezca con el tiempo dejando solamente el movimiento permanente que está dado por la ecuación X_P.

Representación gráfica:

Figura F5-18

Factor dinámico de amplificación (Factor de amplificación o índice de amplitud).-

[5.4.2.1.0.11]

También:

[5.4.2.1.0.12]

En la ecuación 5.4.2.1.0.12 se puede observar que la amplificación dinámica varía con la razón de frecuencia y con la razón de amortiguamiento .

Cuando la amplitud se hace infinita y se dice que el sistema está en resonancia, que tiene aplicación en la acústica, electrónica y física nuclear, pero es completamente perjudicial en el campo de las estructuras, especialmente en los puentes, los cuales por su baja frecuencia entran fácilmente en resonancia bajo la acción de los vientos prolongados o la acción de cargas cíclicas.

Grafico de curvas paramétricas de amplificación dinámica

Grafico de ángulo de fase en función de la razón de frecuencia

En el gráfico:

Carga estática.- . La carga estática es independiente del amortiguamiento.

Resonancia.- La amplitud es sustancialmente amplificada cuando el coeficiente de amortiguamiento viscoso es bajo.

Excitación de alta frecuencia.- . La masa permanece esencialmente estacionario debido a su inercia, sin importar el amortiguamiento de su movimiento.

b).- Movimiento armónico de apoyo.- La causa de las vibraciones forzadas no tiene por qué ser exclusivamente una fuerza periódica aplicada directamente a la masa del sistema. Ya que en muchos sistemas, tales como las suspensiones de automóviles, las vibraciones forzadas las originan el movimiento periódico del soporte en que se apoya el sistema y no una fuerza aplicada directamente. En la ecuación 5.4.2.1.0.2, tenemos las ecuaciones diferenciales correspondientes, cuya solución es similar a lo tratado para fuerzas armónicas.

Para su solución basta con reemplazar F₀ por Kb

Ejemplo de movimiento oscilatorio de apoyo

Ejemplo ilustrativo.- El pórtico de acero mostrado en la figura soporta una máquina rotante que produce una fuerza horizontal F(t) = 1000 sen 5.3 t (N), Suponiendo un 5% de amortiguamiento crítico, determine: a) la amplitud permanente de vibración y b) la fatiga dinámica en las columnas. Considere que el miembro superior de pórtico es rígido. El modulo de la sección de las columnas es s = I/C= 288 m3 y el modulo de elasticidad E para el acero es 210 GN/m2.

Solución

1).- El modelo discretizado es:

2).- Cálculo de los parámetros de este movimiento.-

a).- Del K_e (ver tabla de rigideces de resorte, para viga en voladizo):

b).- De la deformación estática:

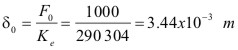
c).- De la frecuencia natural:

d).- De la razón de amortiguamiento y la razón de frecuencia:

3).- Cálculo de la amplitud permanente:

4).- Cálculo de la fuerza cortante máximo en las columnas:

5).- Cálculo del momento máximo en las columnas:

6).- Cálculo de la fatiga máxima:

5.4.2.2.- Para fuerzas de excitación polinomial.- Es importante en las aplicaciones, por que muchas funciones se pueden aproximar con polinomios en un intervalo dado del tiempo. En este caso, obtendremos la solución particular de la ecuación diferencial (de la misma manera se realiza para vibraciones forzadas sin amortiguamiento), buscando una solución de la misma forma (conjetura sensata).

Dado:

Donde:

(son constantes dadas)

Solución particular:

Donde:

(son constantes por determinar)

Ejemplo, si su ecuación diferencial está dada por 5.4.2.1.0.1:

[]

Solución particular es:

Derivándole dos veces, con respecto al tiempo y reemplazándolos en []:

Los coeficientes de potencia, deben ser nulos:

Luego: