IV CINÉTICA DE UN CUERPO RÍGIDO EN MOVIMIENTO PLANO

4.1.- INTRODUCCIÓN.- Se aplica las Leyes de Euler; la primera Ley gobierna el movimiento del centro de masa, que representa al movimiento de traslación del cuerpo y la segunda Ley gobierna el movimiento rotacional del cuerpo rígido, en términos de la cantidad del movimiento angular (momento cinético, ímpetu angular o momentum angular), está cantidad incluye los momentos y productos de inercia de masa del cuerpo, y su movimiento angular.
Entendiendo al momento de inercia de masa, como una medida de la resistencia de un cuerpo a acelerarse angularmente respecto al un eje en , y la masa, como una medida de la resistencia del cuerpo a acelerarse linealmente en el marco de referencia .

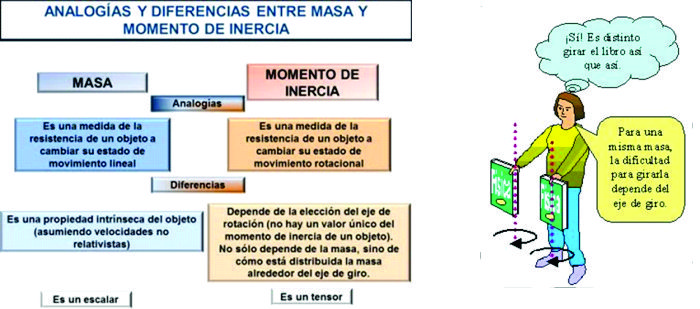
Ejemplo:

4.2.- CANTIDAD DE MOVIMIENTO ANGULAR DE UN CUERPO RÍGIDO.-

Por definición el momento cinético de la masa diferencial, con respecto a A es:

Para el cuerpo, el momento cinético con respecto a A es:

La velocidad de la masa diferencial, es:

En 4.2.0.0.0.1:

Como, es único:

4.2.1.- Considerando tres casos, (para 4.2.0.0.0.2).-

4.2.1.1.- Si, A es un punto fijo o extensión rígida de .- Entonces , y usando "O" para designar dicho punto, se tiene:

4.2.1.2.- Si, A es el centro de masa de .- Entonces , y usando "G" para designar dicho punto, se tiene:

4.2.1.3.- Si, A es un punto cualquiera diferente del punto fijo o centro de masa ("O" o "G").

Si, se tiene de la figura F4-2:

En 4.2.0.0.0.2:

Podemos encontrar lo deducido también, de la cinética de un sistema de partículas.- Sabiendo de la ecuación 3.5.1.5.0.2:

4.2.2.- Cuerpo Rígido en movimiento plano:

Sea:

A Origen del sistema de coordenadas cartesianas (xyz).

XY Plano de referencia del movimiento (paralelo con xy).

Velocidad de "P" de masa diferencial "dm", que es la misma la de su punto acompañante Q en el plano de referencia.

y

En 4.2.0.0.0.2:

Donde:

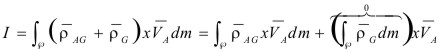
Donde:

(Producto de inercia de masa de , respecto a los ejes x e z a través de "A")

(Producto de inercia de masa de , respecto a los ejes y e z a través de "A")

(Momento de inercia de la masa de , respecto al eje z a través de "A")

Por lo tanto:

4.2.3.- Puntos convenientes, para el estudio del movimiento en el plano.- En 4.2.2.0.0.1

a).- Si, A es un Punto fijo o extensión rígida de .- Entonces , usando "O" para designar dicho punto, se tiene:

b).- Si, A es el centro de masa de .- Entonces , usando "G" para designar dicho punto se tiene:

c).- Si, A es el centro instantáneo de velocidad nula.- Entonces , usando "Ci" para designar dicho punto se tiene:

Ver momentos de inercia de formas geométricas comunes

d).- Si, A es un punto cualquiera y están con el centro de masa G en un mismo plano, y el cuerpo es simétrico con el plano de movimiento de G:     Donde:   d brazo de palanca de

Figura F4-2.3

Leer el Capitulo IV del Libro