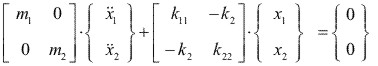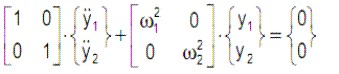5.6.- Introducción a Vibraciones de Sistemas de 2 Grados de Libertad

5.6.1.- Introducción.

Se dice que un sistema tiene dos grados de libertad, cuando se requieren dos coordenadas independietes para describir su movimiento. El estudio de estos sistemas sirve de paso previo para entender el funcionamiento de los sistemas de varios grados de libertad.

Hasta el momento, se han estudiado los sistemas con 1 gdl viéndose que:

Los sistemas con 2 gdl presentan importantes diferencias respecto a los sistemas con 1 gdl; de hecho, su comportamiento es cualitativamente muy similar al de un sistema con N gdl. Sin embargo, si bien los conceptos matemáticos y físicos que aparecen en los sistemas con 2 gdl son idénticos a los de sistemas con N gdl, tienen la ventaja de que sus ecuaciones algebraicas son todavía relativamente manejables y los ejemplos accesibles. Permiten, por ello, una formulación analítica sencilla y no dependiente del álgebra matricial.

Se verá como si un sistema con 2 gdl sin amortiguamiento es desplazado de su posición de equilibro y dejado en libertad, no siempre realiza un movimiento armónico y ni tan siquiera periódico, sino sólo para determinadas formas (tantas como gdl) de perturbar el equilibrio. Sólo para dos tipos (2 gdl) de perturbaciones el movimiento subsiguiente es armónico y, en general, con distinta frecuencia para cada tipo de perturbación.

Un sistema con 2 gdl tendrá, por lo tanto, dos frecuencias naturales y, sometido a una excitación armónica, llegará a la condición de resonancia para dos frecuencias de excitación diferentes. El estudio del comportamiento dinámico de este tipo de sistemas facilitará la introducción de conceptos como respuesta síncrona, frecuencias y modos naturales de vibración y análisis modal.

5.6.2.- Ecuaciones del movimiento: Formulación matricial

Consideremos el sistema de la figura.

Aplicando la segunda ley de Newton a cada una de las masas:

Ecuaciones diferenciales, que no son independientes y constituyen un sistema ya que ambas incógnitas x_{1 (t)} y x_{2 (t)} aparecen en las dos, y pueden expresarse matricialmente:

o, de forma más abreviada, con notación matricial:

Las matrices [M], [C] y [K], llamadas respectivamente matriz de inercia, matriz de amortiguamiento y matriz de rigidez, son simétricas, como se puede observar.

Se observa, además, en este ejemplo que la matriz [M] es diagonal. Esta es una característica de los sistemas de parámetros discretos que no se presenta en muchas otras ocasiones. Si en la expresión las tres matrices [M], [C] y [K] fueran diagonales, las dos ecuaciones serían independientes o estarían desacopladas, siendo en tal caso resolubles cada una de ellas por las técnicas desarrolladas para los sistemas con 1 gdl.

5.6.3.- Vibraciones libres no amortiguadas. Modos de vibración.-

La resolución del problema de vibraciones libres no amortiguadas permitirá la determinación de los parámetros modales característicos del sistema de dos grados de libertad: sus dos frecuencias naturales y sus dos modos naturales de vibración.

Suponiendo que no hay fuerzas exteriores aplicadas al sistema y que los términos disipativos de energía son nulos, el sistema de ecuaciones del movimiento se reduce a (k₁₁= k₁ + k₂, k₂₂= k₂ + k₃):

La solución de este sistema de ecuaciones diferenciales puede abordarse por distintos procedimientos. Estando interesados en la posibilidad de que el sistema realice un movimiento armónico síncrono (tiene lugar en un sistema constituido por dos o más masas y caracterizado por que todas ellas vibran, en fase, con la misma frecuencia), se supondrán, análogamente como se hacía con sistemas de 1 gdl; soluciones de la forma:

Derivándoles respecto al tiempo:

Sustituyendo, se obtendrán dos ecuaciones:

lo que constituye un sistema de ecuaciones en X₁ y X₂. Para que dicho sistema tenga solución distinta de la idénticamente nula, se tendrá que cumplir que el determinante del sistema sea nulo. Desarrollando el determinante y ordenando, se obtiene una ecuación bicuadrática cuyas raíces son:

Si son las dos soluciones de la ecuación, sólo podrá tener lugar movimiento armónico en estas dos frecuencias que son las frecuencias naturales del sistema.

El sistema de dos ecuaciones en X₁ y X₂ puede ponerse, a su vez, en la forma:

Sustituyendo en cualquiera de estas expresiones los valores de se determina la relación existente entre las amplitudes de los movimientos de las dos masas. Los movimientos síncronos que cumplen esta relación de amplitudes son armónicos, y reciben el nombre de modo natural de vibración. Hay dos modos naturales, uno para cada frecuencia, . Al desplazar el sistema de su posición de equilibrio según un modo natural y soltarlo, comenzará a oscilar libre y armónicamente a la frecuencia del modo.

Se puede demostrar que, ambos modos son ortogonales entre sí respecto a las matrices de inercia y rigidez; es decir:

Como las dos amplitudes de un modo no están determinadas más que en la relación existente entre ellas, es una práctica habitual el normalizar los modos de forma que:

5.6.4.- Coordenadas naturales. Introducción al Análisis Modal

Coordenadas Naturales.- Es el sistema de coordenadas resultanta de aplicar al sistema mecánico a estudio un cambio de coordenadas basado en la matriz de modos :

En estas nuevas coordenadas , el sistema de N ecuaciones diferenciales con N incógnitas se desacopla y trasforma en N ecuaciones de una sola incógnita, es decir, en N problemas de 1 gdl.

Luego, para el Análisis Modal:

Teniendo en cuenta las ortogonalidades y ortonormalidad resulta:

o bien, teniendo en cuenta que las matrices presentes son diagonales:

Estas dos ecuaciones son independientes, y puede cada una de ellas resolverse con los métodos estudiados para los sistemas con 1 gdl.

A las coordenadas y₁(t) e y₂(t), definidas con este cambio de variable se les denomina coordenadas naturales, y en ellas las ecuaciones del movimiento están desacopladas. El método seguido a la hora de desacoplar las ecuaciones del sistema constituye la técnica de análisis modal

Cabría ahora, por tanto, pensar en la posibilidad de estudiar las vibraciones libres con amortiguamiento. Pero surge entonces una nueva dificultad por el hecho de que, en general, esta transformación de coordenadas, que diagonaliza las matrices de rigidez e inercia, no hace lo mismo con la matriz de amortiguamiento. Este caso no se estudiará ahora, pero se puede considerar incluido en el que se realizará posteriormente (curso de antisísmica) para sistemas de N gdl.

5.6.5.- Vibraciones forzadas. Condiciones de resonancia

Se estudia el caso en que no existe amortiguamiento, y se prescindirá también de la componente de la respuesta debida a las condiciones iniciales (sin amortiguamiento, esta componente no desaparecerá nunca, pero como ya se han estudiado las vibraciones libres, se prescindirá de ellas en virtud del Principio de Superposición).

Supóngase actuando sobre el sistema una excitación armónica síncrona de modo que las ecuaciones diferenciales del movimiento del sistema respondan a la expresión:

Suponiendo soluciones en la forma sustituyendo estos valores y sus derivadas segundas en la ecuación anterior y reordenando, se obtiene el siguiente sistema de dos ecuaciones con dos incógnitas:

Aplicando la regla de Cramer para resolver este sistema de ecuaciones se obtienen los valores de las amplitudes de los movimientos armónicos que se están buscando:

[5.6.5.3]

que pueden expresarse:

[5.6.5.4]

amplitudes que se hacen infinitas cuando la frecuencia de excitación coincide con cualquiera de las dos frecuencias naturales. Por lo tanto, un sistema de 2 gdl tiene dos condiciones de resonancia.

En el ejemplo representado en la Figura F5-5.1, pueden apreciarse las amplitudes de los movimientos de las dos masas para diferentes valores de la frecuencia de excitación, observándose claramente la presencia de dos resonancias alrededor de las frecuencias de 8 y 12 Hz, aproximadamente.

Considérese ahora el caso en el que hay amortiguamiento viscoso lineal. En el caso más general, las ecuaciones de equilibrio serán:

Haciendo como antes y suponiendo soluciones de la forma:

Se obtendrá:

Donde,

son las llamadas impedancias mecánicas.

Despejando por la regla de Cramer X₁ y X₂ de la expresión matricial del sistema de ecuaciones y teniendo en cuenta que la matriz de impedancias es simétrica

expresiones que se suelen escribir en la forma

donde los términos representan algo análogo al papel que la función de transferencia desempeñaba en los sistemas con 1 gdl. Así, a la matriz [H] se la denomina matriz de transferencia.

Mediante la ecuación anterior se puede estudiar la respuesta estacionaria de cualquier sistema ante unas fuerzas armónicas síncronas de amplitudes conocidas.