5.3.2.- Vibraciones libres con amortiguamiento.- Los movimientos oscilatorios tienden a disminuir con el tiempo hasta desaparecer. Esto se debe al amortiguamiento que se presenta, el cual hace que parte de la energía se disipe. Las causas de este amortiguamiento están asociadas con diferentes fenómenos dentro de los cuales se puede contar la fricción de la masa sobre la superficie de apoyo, el efecto del aire que rodea la masa, el cual tiende a impedir que ocurra el movimiento, la no linealidad del material del resorte, entre otros. Existen numerosas maneras de describir matemáticamente el efecto de fricción. Dentro de estos modelos, uno de los más utilizados es el que se conoce como amortiguamiento viscoso.

La ecuación diferencial para este tipo de movimiento será:

Siendo:

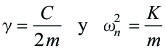
El parámetro indica la intensidad del rozamiento y es la frecuencia que tendría el oscilador si no hubiera rozamiento y recibe el nombre de frecuencia natural.

Solución de la ecuación diferencial.

La ecuación que determina el movimiento de la masa es la del oscilador armónico con un término añadido proporcional a la velocidad, que representa el rozamiento al que está sometida la masa. Es una ecuación diferencial de coeficientes constantes. La técnica para resolver este tipo de ecuaciones es buscar soluciones de la forma:

La idea es que al derivar esta función; el resultado es ella misma multiplicada por el parámetro r.

Donde, A es una constante arbitraria y "r" es un parámetro o raíz característica.

Derivando dos veces 5.3.2.0.0.2 respecto al tiempo, se tiene:

Sustituyendo 5.3.2.0.0.2 y 5.3.2.0.0.3 en 5.3.2.0.0.1:

(Ecuación característica)

Resolviendo la ecuación característica

a).- Para el caso en que , las raíces son distintas y si llamamos r₁ y r₂, la solución general de 5.3.2.0.0.1 será:

b).- Para el caso en que , hay solo una raíz repetida r y la sustitución directa mostrará, que hay una solución de la ecuación 5.3.2.0.0.1:

5.3.2.1.- Movimiento críticamente amortiguado (amortiguamiento crítico).- Se da cuando el discriminante se anula, haciendo que la constante C reciba el nombre de coeficiente de amortiguamiento crítico .

El coeficiente de amortiguamiento real "C" y el crítico "C_C" están relacionados por el factor de amortiguamiento relativo (razón de amortiguamiento o factor amplificador o índice de amortiguamiento) " " (eta) o "" (zeta), de la siguiente manera:

5.3.2.1.0.1 en 5.3.2.1.0.2:

5.3.2.1.0.3 en 5.3.2.0.0.4:

Para el movimiento críticamente amortiguado , que no pertenece a un movimiento vibratorio. Para este caso, el sistema retorna a su posición de equilibrio sin vibrar en el menor tiempo posible

Para este caso la solución de 5.3.2.0.0.1 está dada por 5.3.2.0.0.6:

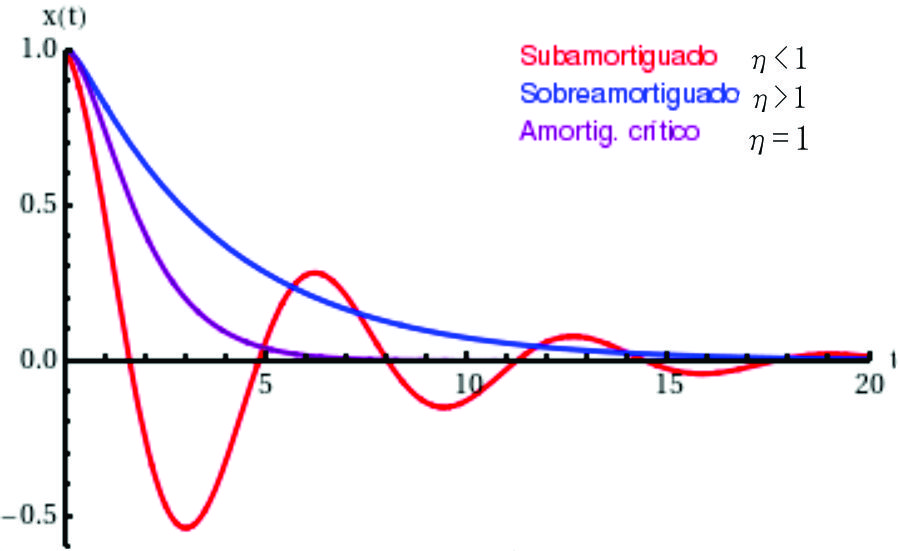
Representación gráfica de los distintos movimientos:

5.3.2.2.- Movimiento sobreamortiguado (amortiguamiento fuerte o supercrítico).- Se da cuando el discriminante tiene un valor real, luego y la solución de 5.3.2.1.0.1 está dado por 5.3.2.0.0.5

El sistema retorna a su posición de equilibrio sin vibrar en un tiempo mayor, que el que, se produce cuando el amortiguamiento es crítico.

5.3.2.3.- Movimiento subamortiguado o movimiento vibratorio amortiguado (amortiguamiento débil o sub crítico).- Se da cuando el amortiguamiento es pequeño, haciendo que el discriminante tenga raíces complejas conjugadas, luego (sub crítico):

(i = - 1 unidad imaginaria)

En 5.2.2.2.0.5:

Considerando las relaciones de Euler:

Se anula las raíces de las cantidades imaginarias: 5.3.2.3.0.2 en 5.3.2.3.0.1:

En 5.3.2.3.0.1 llamamos a la frecuencia angular del sistema (frecuencia de las oscilaciones amortiguadas o pulsación propia amortiguada), definido por la siguiente relación:

El valor del coeficiente de amortiguamiento en estructuras reales es considerablemente menor que el coeficiente crítico de amortiguamiento; generalmente fluctúan entre el 2% y el 20% del valor crítico. Sustituyendo este valor máximo, = 0.20 en la ecuación 5.3.2.3.0.4 da:

De este resultado se puede observar que la frecuencia de vibración de un sistema con un coeficiente de amortiguamiento alto como del 20% del amortiguamiento crítico, es prácticamente igual, a la frecuencia natural de un sistema sin amortiguamiento, Por esta razón, en la práctica, la frecuencia natural de un sistema con amortiguamiento se considera igual a la frecuencia calculada en el sistema sin amortiguamiento. {Para pequeños (usado mucho en la ingeniería)}.

La ecuación 5.3.2.3.0.3, también se pude expresar de la siguiente manera:

Donde :

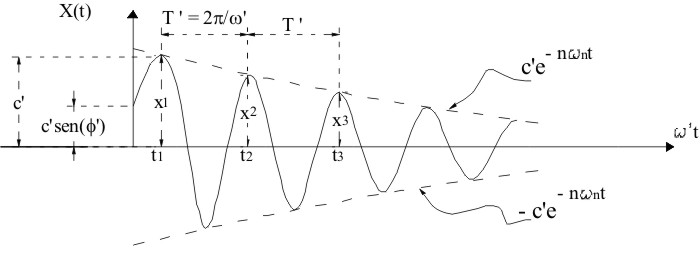
Con una amplitud decreciente limitada por las curvas , como se ve en la representación gráfica:

Figura F5-3.2.2

(periodo amortiguado), (frecuencia amortiguada) y son constantes (independientes del tiempo), aún cuando no lo sea la amplitud, ya que, la amplitud máxima del movimiento disminuye con el tiempo debido al factor .

Decremento logarítmico (DL).-

El amortiguamiento viscoso lineal no es un elemento físico real, en muchos sistemas físicos, sino un concepto matemático que se utiliza para explicar la disipación de energía. Por esta y otras razones, suele ser necesario determinar experimentalmente el valor de (razón de amortiguamiento). Esto se logra fácilmente midiendo el desplazamiento en dos "picos" sucesivos del movimiento, por ejemplo, si se tiene con (la intersección de las curvas no se dan en el mismo punto en sus valores máximos, al desvió se le considera insignificante):

Tomando logaritmos neperianos de uno y otro miembro y llamándole decremento logarítmico , que viene a ser la cantidad de amortiguamiento presente en un sistema que, consiste en medir la razón de caída:

Donde :

(Periodo de la vibración libre amortiguada)

Cuando el amortiguamiento del sistema es pequeño, los desplazamientos serán casi iguales , con lo que será muy pequeño, entonces , con lo que o sea .

Nota.- Si los valores de X₁ y X₂ son tan próximos que es prácticamente imposible distinguirlos experimentalmente, las fórmulas anteriores pueden modificarse para utilizarse con dos amplitudes separadas n ciclos.

Ejemplo ilustrativo.-

Una plataforma que pesa w = 20 kN está soportada por cuatro columnas empotradas en los cimientos y en la plataforma. Se ha determinado, experimentalmente, que una fuerza estática horizontal, F = 5 kN, aplicada a la plataforma, produce un desplazamiento = 0.05 cm. También se ha estimado que el coeficiente de amortiguamiento es del orden del 5% del amortiguamiento crítico. Determine para esta estructura lo siguiente: a) la frecuencia natural sin amortiguamiento, b) el coeficiente de amortiguamiento, c) el decremento logarítmico, y d) el número de ciclos y el tiempo requerido para que la amplitud del movimiento se reduzca desde un valor inicial de 0.3 cm a 0.03 cm.

Solución

1).- El modelo discretizado de la plataforma, es:

2).- D.C.L.:

3).- Cálculo del coeficiente de rigidez equivalente.- El coeficiente de rigidez que viene a ser la fuerza por unidad de desplazamiento, se obtiene de la siguiente manera:

4).- Cálculo de la frecuencia natural:

5).- Cálculo del coeficiente de amortiguamiento:

Si:

Luego, el coeficiente de amortiguamiento es:

6).- Cálculo del decremento logarítmico.- Es aproximadamente (el coeficiente de amortiguamiento es pequeño con respecto al crítico) a:

y la razón de dos amplitudes consecutivas máximas, es:

7).- Cálculo del número de ciclos y el tiempo correspondiente:

Si, la razón entre la primera amplitud X₀ y la amplitud X_k, después de k ciclos, puede expresarse como:

Tomando logaritmos naturales:

La frecuencia con amortiguamiento, está dado por:

y el periodo T', por:

Por lo tanto, el tiempo para 8 ciclos es: