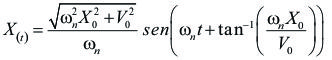5.3.- VIBRACIONES LIBRES DE TRASLACIÓN DE UN GRADO DE LIBERTAD

Son aquellas vibraciones que se producen sin cargas externas, bajo la acción de la energía potencial de las fuerzas elásticas y fuerzas inerciales. Las vibraciones libres pueden ser sin amortiguamiento y con amortiguamiento, produciéndose el amortiguamiento como consecuencia de las fuerzas internas del material y debido al medio externo.

Es la que ocurre cuando un sistema oscila bajo la acción de fuerzas inherentes al sistema mismo, es decir, cuando no actúa ninguna fuerza externa, esto se da, cuando la fuerza perturbadora o el desplazamiento , que se indican en las ecuaciones 5.2.1.0.0.1 y 5.2.2.0.0.1 son nulas. Describiendo el movimiento y la respuesta de la masa m cuando se suelta de una posición que no es la del equilibrio. Siendo de gran importancia su frecuencia natural (en función de la masa y rigidez del sistema).

Si para el estudio, se tiene un sistema discretizado de parámetros localizados formado por una masa concentrada conectada a un marco inercial, por medio de un resorte de constante "K" y un amortiguador "C", y el sistema es de un grado de libertad.

Ejemplo de movimiento oscilatorio libre

Ver otro ejemplo con dos tipos de amortiguamiento haga click aqui

5.3.1.- Vibraciones libres no amortiguadas.- Es el sistema más simple y fundamental, donde "ignoramos" o despreciamos las fuerzas de amortiguamiento, por lo que, el sistema en movimiento estará gobernado sólo por la influencia de las llamadas condiciones iníciales, o sea el desplazamiento y la velocidad especificados en el instante t = 0, cuando se inicia el estudio del movimiento del sistema.

Luego: , en este caso la masa vibra sin pérdida de energía y la ecuación diferencial de su movimiento será:

Ecuación diferencial homogénea lineal de segundo orden

Ejemplos de M.A.S.

Pincha sobre la masa y sepárala de la posición de equilibrio, se produce un movimiento armónico simple. Puedes variar la frecuencia de oscilación. Se representan la posición, velocidad, aceleración, energía cinética y energía potencial en función del tiempo, despreciando el rozamiento.

a).- Solución de la ecuación diferencial.- La solución de esta ecuación se puede escribir como:

Esto describe un movimiento oscilatorio de frecuencia y amplitud c. se denomina frecuencia circular natural, determina el intervalo de tiempo en el que la función se repite. , denominada fase, determina el valor inicial de la función sinusoidal. La fase se mide en radianes (rad), mientras que la frecuencia se mide en radianes por segundo (rad/s).

Para verificar que la ecuación [ sea efectivamente una solución de la ecuación de movimiento, la sustituimos en la ecuación [5.3.1.0.0.1]:

Esta última ecuación se satisface si:

La raíz positiva se le conoce como la frecuencia circular natural del sistema o también como pulsación propia no amortiguada o simplemente como la pulsación de la vibración.

Las constantes y c, están definidas por las condiciones iniciales del problema. Consideremos que el resorte se encuentra en una posición X₀ en t = 0, la fuerza inicial kX₀ va a iniciar el movimiento. Si adicionalmente conocemos la velocidad inicial V₀, tenemos que:

Resolviendo ambas ecuaciones se obtiene:

Por lo tanto, la solución de la ecuación de movimiento para el sistema masa-resorte es:

Esta solución se ilustra en la figura a continuación:

Figura F5-3.1b: Solución de la ecuación de movimiento para un sistema de un grado de libertad

Utilizando las siguientes relaciones trigonométricas:

la solución de la ecuación de movimiento 5.3.1.0.0.2 se puede escribir como:

En la ecuación 5.3.1.0.0.2, el tiempo aumenta de en , o sea la función se repite cada , por lo tanto el periodo es:

La frecuencia natural es:

Debido a que la cantidad sólo difiere de la frecuencia natural en el factor constante , también algunas veces se la denomina frecuencia natural. Para distinguir entre estas dos expresiones de la frecuencia natural, se puede llamar a frecuencia circular o angular.

También tomamos en cuenta, que:

y

La velocidad y la aceleración se obtendrán derivando la ecuación 5.3.1.0.0.5:

La ecuación 5.3.1.0.0.5, también se puede escribir, como:

Donde, concluimos en 5.3.1.0.0.5 y 5.3.1.0.0.8:

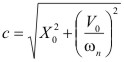y ,

c).- Frecuencia natural en función de la deflexión estática.-

Donde :

Deflexión estática.

Nota.- Si la masa se encuentra colgada del resorte o verticalmente, se obtiene los mismos resultados, por que el origen de la elongación es la posición de equilibrio y no el de la deformación nula del resorte.

Ejemplo animado de un M.A.S. (con el mouse desplace la masa y luego sueltalo):

En la figura F5-3.1c se ilustran tres sistemas de un grado de libertad (que desarrollaremos más adelante). Para estos casos se obtienen las siguientes frecuencias naturales y periodos de oscilación:

Masa-Resorte

 

 

Disco y eje

 

 

Péndulo simple

 

 

 

Figura F5-3.1c: Ejemplos de sistemas de un grado de libertad (pequeñosdesplazamientos)

 

Ejemplos ilustrativos:

1.- Determine la frecuencia circular natural del sistema mostrado en la figura, que consiste en una carga de 1 kN aplicada a una viga en voladizo a través de un resorte K₂. La viga (con un extremo empotrado) tiene un espesor e = 0.5 cm, un ancho b = 5 cm, un módulo de elasticidad E = 210 GN/m² y una longitud L = 50 cm. La constante del resorte es K₂ = 2 kN/m.

Solución

1).- El modelo discretizado del sistema es:

2).- D.C.L.:

3).- Cálculo del K_e del sistema:

a).- Desplazamiento producido por una fuerza estática P aplicada al extremo libre de una viga en voladizo, está dado por:

Donde I es el momento de inercia de la sección de la viga.

b).- Constante del resorte equivalente K₁ de la viga:

(Ver también tabla de rigideces de resorte)

Donde: (para una sección rectangular)

c).- Constante equivalente K_e del sistema.- La viga y el resorte de este sistema están conectados como resortes en serie, en consecuencia, la constante del resorte equivalente del sistema está dada, por:

Reemplazando valores, se tiene:

Luego :

4).- Cálculo de la frecuencia natural del sistema.- Si la frecuencia circular natural del sistema está dado por:

Luego :

2.- Una mansa de 8 Kg se desliza por una superficie horizontal exenta de rozamiento, según indica la figura animada y sus animaciones.

Los dos resortes están sometidos a tracción en todo momento y las poleas son pequeñas y exentas de rozamiento. Si se desplaza la masa 25 mm hacia la derecha de su posición de equilibrio y se suelta con una velocidad de 800 mm/s hacia la derecha cuando t = 0 determine:

Solución

1).- D.C.L. (s):

a).- En la posición de equilibrio.

(a)

b).- En Movimiento.

(b)

2).- Relaciones cinéticas.

En (a):

En (b):

(1) en (2) obtenemos:

Operando y reemplazando valores:

Luego:

Sabemos:

Dividiendo (4) entre (5):

Se conoce que:

y

Luego:

Sabemos también:

Reemplazando datos obtenemos:

Resolviendo la ecuación tenemos que:

3.- El hilo ligero atado al bloque de 50 N de la figura esta arrollado a un cilindro uniforme de 35 N. Si el hilo no se desliza por el cilindro, escribir la ecuación diferencial del movimiento para la posición y(t) del bloque de 50 N y determinar la frecuencia y el periodo del movimiento vibratorio resultante.

Solución

1).- D.C.L. (s) del bloque y el cilindro:

a).- En la posición de equilibrio.

(a)

(b)

b).- En Movimiento.

(c)

(d)

2).- Relaciones cinemáticas.

3).- Relaciones cinéticas.

En (a):

En (b):

En (c):

En (d):

Reemplazando (4) en (3) tenemos:

Reemplazando en (5):

" Reemplazando datos en la ecuación anterior obtenemos:

5.3.1.1.- Por el principio de conservación de energía.- Como en los sistemas no amortiguados, no existe disipación de energía, es decir que está se conserva, la ecuación 5.3.1.0.0.1 se puede obtener a partir de este principio

Para una posición "X" cualquiera del movimiento de m, se tiene:

5.3.1.2.- Método de RAYLEIGH.

En un sistema que evoluciona bajo la acción de Fuerzas conservativas sabemos que la energía total del sistema se mantiene constante.

Analicemos el sistema masa resorte haciendo consideraciones energéticas:

c = define un punto cualquiera del resorte.

c = 0, la elongación es 0.

c = L, la elongación es X.

La función elongación es:

Analizaremos en primer lugar considerando parámetros concentrados (es decir que la masa está concentrada en la punta del resorte y que la masa del resorte no influye).

Energía cinética:

Como la única porción del sistema que tiene masa es el cuerpo colgado del resorte entonces será la única porción que tendrá energía cinética, por ende la función oscilación nos interesará únicamente en el extremo:

Hallando la derivada:

Introduciendo esta función en la ecuación de la energía cinética:

Ahora calcularemos la energía potencial elástica:

Pero como bien sabemos:

La energía cinética total del sistema es cero en el desplazamiento máximo y es máxima en el punto de equilibrio estático. Para la energía potencial del sistema ocurre lo contrario. Por tanto:

Y como la Energía mecánica es cte.

Energía total del sistema

Despejando de la ecuación, llegamos a la expresión de la frecuencia natural de oscilación del sistema considerando parámetros concentrados:

Entonces vemos que el método de la energía nos permite calcular la frecuencia natural del sistema.

5.3.1.3.- Vibraciones libres de los sólidos rígidos.- El análisis de las vibraciones de un cuerpo rígido o de un sistema de cuerpos rígidos con un grado de libertad es similar al análisis de la vibraciones de una partícula. La posición del cuerpo, o del sistema de cuerpos, se define en función de una variable adecuadamente elegida, un desplazamiento X o un ángulo ; seguidamente, se escribe una ecuación que relaciona esa variable con una segunda derivada en el marco de referencia elegido. La ecuación obtenida es de la misma forma que la 5.3.1.0.0.1, es decir, si tenemos:

A los parámetros obtenidos de estas ecuaciones se les llama efectivos.

Por ejemplo tenemos, un cuerpo rígido con movimiento alrededor de un eje fijo.- Si las fuerzas de fricción son despreciables.

Solución

1).- D.C.L.:

2).-Relaciones cinéticas, para un instante cualquiera:

Está ecuación diferencial no es lineal, por que "sen" es una función no lineal, pero si nos limitamos a considerar ángulos muy pequeños para los cuales la ecuación [], se vuelve lineal (solución aproximada), luego:

Es una función armónica simple

Luego :

Donde :

[]

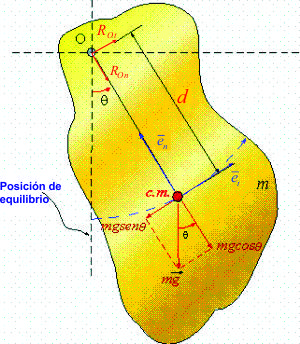
El campo gravitacional proporciona la acción restauradora y la frecuencia circular natural es proporcional a .

Nota.- Para soluciones exactas, se tienen factores de corrección del periodo (tablas), al encontrar el centro de oscilación o sea al igualarlo con en péndulo simple de longitud al centro de percusión encontrado . Se prescinde de los factores de corrección para ángulos menores a 10°.

Ejemplo de moviniento vibratorio de un cuerpo rígido:

5.3.2.- Vibraciones Torsionales.- La ecuación del momento respecto a un eje fijo, de un cuerpo obligado a girar sobre el eje fijo mencionado, es:

Si M_z es un momento recuperador lineal. Por ejemplo, consideraremos un disco circular fijado al extremo de un eje ligero como se muestra en la figura F5-3.2a

Figura F5-3.2a

Si Mediante un agente externo, se hace girar el disco alrededor de la directriz A-A del eje, entonces el disco girará esencialmente como un sólido rígido, mientras que el eje, como es mucho más delgado y largo, girará y proporcionará un par recuperador sobre el disco que intentará que éste vuelva a su posición inicial.Al considerar los posibles movimientos de un sistema de este tipo perturbado de la manera mencionada, idealizamos el problema concentrando toda la acción elástica en el eje y todos los efectos inerciales en el disco. A partir de la resistencia de materiales sabemos que para un eje circular transversal constante la cantidad de giro inducida por un momento M_z es, dentro del rango elástico de deformaciones,

donde G es el módulo de rigidez transversal, o de cizalladura, del material que compone el eje, J es el momento de inercial polar del área de la sección transversal del eje, y L es la longitud del eje. Podemos desarrollar el concepto de constante de muelle torsional K_t dada como:

Para el caso que estamos estudiando, tenemos:

Así, en este análisis el eje delgado juega el mismo papel que el ligero resorte lineal, podemos expresar la ecuación diferencial resultante, como sigue:

Nótese que la forma de la ecuación es idéntica a la ecuación de los movimientos lineales. En consecuencia, todas las conclusiones desarrolladas en ese análisis se puede aplicar ahora con los cambios de notación adecuados. De esta forma, el disco, una vez perturbado mediante la imposición de un movimiento angular, tendrá una frecuencia de oscilación torsional natural de rad/s. La ecuación del movimiento para el disco es:

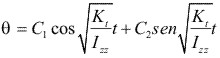
donde C₁ y C₂ son constantes de integración a determinar a partir de las condiciones inerciales. De esta forma, si y para t = 0 tenemos:

En el ejemplo que acabamos de presentar, el momento recuperador lineal proviene de un largo eje delgado. Podría haber otros agentes que puedan desarrollar un momento recuperador lineal sobre un sistema que, de otra forma, giraría libremente alrededor de un eje fijo en un espacio inercial. Hablaríamos entonces de constante de resortes torsionales equivalentes.