5.2.- ESTUDIO DE SISTEMAS DE UN GRADO DE LIBERTAD

Figura F5-2.1: Sistema de un grado de libertad: (a) fuerza aplicada p(t); (b) movimiento del terreno inducido por un sismo.

5.2.1.- Ecuación diferencial del movimiento de traslación.- Al realizar el modelo discretizado, se asume que cada elemento del sistema representa una sola propiedad; es decir, la masa m que almacena y libera energía cinética, representa sólo la propiedad de inercia y no la elasticidad o disipación de energía, mientras que el resorte K que almacena y libera energía potencial, representa sólo a la elasticidad y no a la inercia o la disipación de energía, y el elemento amortiguador C solamente disipa energía. Se tiene que tener en cuenta que tales elementos "puros" no existen en nuestro mundo físico y que los modelos matemáticos son solamente idealizaciones conceptuales, que nos dan información que se requiere para una adecuada comprensión del comportamiento dinámico del sistema físico, incluyendo las especificaciones de diseño y seguridad.

Cada uno de estos elementos tiene características diferentes de excitación-respuesta; la excitación está en la forma de una fuerza o de un momento, y la respuesta correspondiente del elemento está en la forma de un desplazamiento, velocidad o aceleración. Los elementos de inercia se caracterizan por una relación entre una fuerza aplicada (o momento) y la correspondiente respuesta de aceleración. Los elementos de rigidez se caracterizan por una relación entre una fuerza aplicada (o momento) y el desplazamiento correspondiente (o rotación). Los elementos de disipación poseen como característica una relación entre la fuerza aplicada (o momento) y la respuesta correspondiente de velocidad. La naturaleza de estas relaciones, pueden ser lineales o no lineales. Las unidades asociadas con estos elementos y los símbolos más usados para los distintos elementos se muestran en la siguiente tabla N° 5.2.1:

Tabla N° 5.2.1.- Unidades de las partes que constituyen un sistema vibratorio mecánico y sus símbolos convencionales

Si para el estudio, se tiene un sistema discretizado de parámetros localizados formado por una masa concentrada conectada a un marco inercial, por medio de un resorte de constante "K" y un amortiguador "C", y el sistema es de un grado de libertad.

Figura F5-2.1a

Para resolver el sistema se tiene que tener bien claro los siguientes conceptos :

5.2.1.1.- Fuerzas de rigidez (F₁).- Los elementos de rigidez almacenan y liberan la energía potencial de un sistema.

5.2.1.1.1.- Resortes lineales.-

a).- Resortes de traslación.- Si se aplica una fuerza F a un resorte lineal, como se muestra en la figura F5-2.1b esta fuerza produce un desplazamiento x tal que:

Figura F5-2.1b

i).- Resorte duro.- El comportamiento es tal que, la fuerza requerida para producir una determinada deformación aumenta a medida que el resorte se deforma.

ii).- Resorte lineal.- El comportamiento es tal que, la deformación en el resorte es directamente proporcional a la fuerza aplicada en uno de sus extremos.

iii).- Resorte blando.- El comportamiento es tal que, la fuerza adicional necesaria para producir una nueva deformación disminuye a medida que la deformación de resorte aumenta.

Escogemos el resorte lineal, por ser el que más se adecua a la realidad y de posibilitar el tratamiento del movimiento en forma simple.

b).- Resorte de torsión.- Si se considera un resorte lineal de torsión y se aplica un momento al resorte en uno de sus extremos, mientras el otro extremo del resorte se mantiene fijo, entonces: .

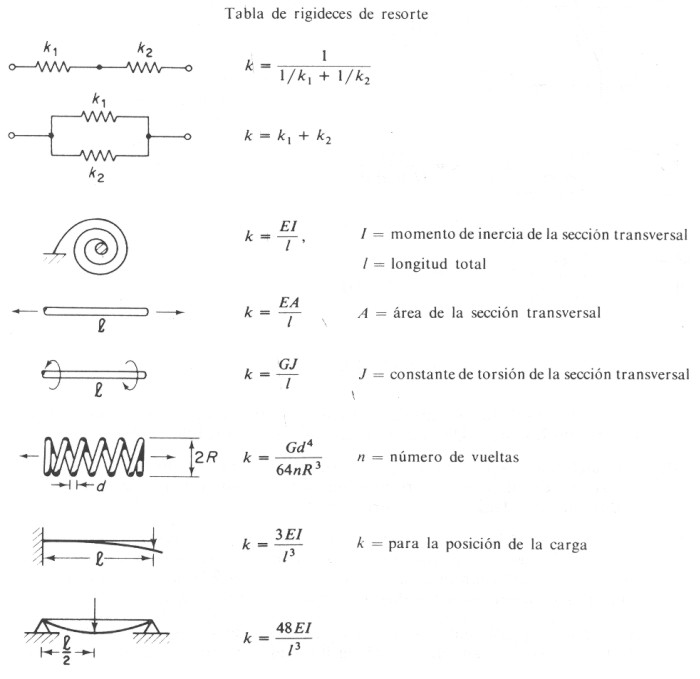
c).- Constante del resorte equivalente de traslación.- Por la teoría de la elasticidad en ciertos estructuras se puede determinar las constantes equivalentes, por ser las deflexiones estáticas muy pequeñas y considerarlas como "lineales", como se ilustra en la siguiente tabla de rigidez equivalentes:

Figura F5-2.1c

5.2.1.1.2.- Resortes no lineales.- Los elementos de rigidez no lineales tienen muchas aplicaciones, sin olvidar los muelles de las suspensiones de los vehículos. En cuanto a un resorte no lineal, la fuerza del resorte F_(x) es una función no lineal de la variable de desplazamiento x. La expansión es una serie de está función, se interpreta como una combinación de componentes de resorte lineales y no lineales, la relación fuerza-desplazamiento se expresa como:

Donde, representa el coeficiente de rigidez del término no lineal desde el punto de vista de la constante del resorte lineal k, puede ser positiva o negativa. Un elemento de resorte para la cual es positiva se llama resorte de endurecimiento (ver figura F5-2.1b) y un resorte para la cual es negativa se denomina resorte de suavización (ver figura F5-2.1b). De acuerdo a la formula mostrada, la energía potencial es:

Nota.- Hay otras formas de resortes no lineales, como son: Resortes cúbicos y resortes lineales, elementos con fluidos, gas comprimido, etc.

5.2.1.2.- Fuerzas de amortiguamiento (F₂).- Fuerza que ejerce el amortiguador sobre la masa m. Se reconoce que es necesario incluir un mecanismo de disipación de energía en la idealización con el fn de caracterizar el decaimiento del movimiento observado.

La descripción real de F₂ es difícil, donde se utiliza modelos ideales de amortiguamiento, que a menudo permiten una satisfactoria predicción de la respuesta esperada.

Las vibraciones sufren un cierto grado de amortiguamiento debido a resistencias en forma de amortiguamiento (amortiguamiento magnético) o a fuerzas de rozamiento (mecánico y fluido); estos últimos pueden ser fuerzas de rozamiento seco o rozamiento de Coulomb entre cuerpos rígidos, o de rozamiento fluido cuando un cuerpo se mueve en el seno de un fluido, o de rozamiento interno entre las moléculas de un cuerpo aparentemente elástico (amortiguamiento sólido y amortiguamiento estructural). De especial interés es el amortiguamiento viscoso producido por el rozamiento fluido a velocidades bajas y medias, que es directamente proporcional y opuesta a la velocidad del cuerpo en movimiento, que instalaremos intencionalmente, permitiéndonos el tratamiento matemático relativamente simple.

5.2.1.3.- Fuerzas de excitación o Cargas Dinámicas (F_(t)).- Son aquellas cargas actuantes en la estructura, cuya magnitud, dirección o posición varía en un intervalo de tiempo relativamente pequeño.

Las deformaciones, fuerzas y esfuerzos, obtenidos como consecuencia de esta acción, también se denominan DINÁMICAS.

Las cargas dinámicas actuantes en las construcciones generan aceleraciones y, como consecuencia, aparecen fuerzas adicionales, denominadas FUERZAS INERCIALES de las masas de estas cargas y de la masa de la estructura en sí, en la cual surgen las vibraciones.

Tipos de excitación Dinámica en estructuras:

Tipos de excitación dinámica

Carga Periódica. Se produce como consecuencia del movimiento de maquinarias y mecanismos, cuya dependencia del tiempo se repite cada cierto período T. Si la carga periódica varía en forma de seno o coseno, entonces tal tipo de carga se denomina vibracional o armónica (ver figura)

Carga de Impacto. Se genera como consecuencia del impacto en un lugar determinado y sus esfuerzos generados dependen de las propiedades elásticas e inerciales de la estructura. Las cargas pueden ser periódicas y no periódicas (ver figuras)

Carga Rodante. Es aquella que cambia su ubicación en la construcción, por ejemplo, el paso de un automóvil, bus, tren por un puente (ver figura) o grúa puente en naves industriales.

Carga de Viento. Son presiones laterales del viento, muy importantes en edificios altos y de grandes luces, dependientes también de la zonificación eólica del proyecto. Las cargas de viento varían por la altura del edificio y en el tiempo de acción (ver figuras)

Carga sísmica. Surge como consecuencia del movimiento desordenado del suelo durante un sismo, el cual genera un movimiento complejo de la cimentación en el tiempo, desplazándose por una determinada ley variable en el tiempo (ver figuras).

Carga Impulsiva. Son cargas súbitas, como las ondas de una explosión, que generan una variación importante de la presión sobre la estructura (ver figuras).

Regresando al problema, considerando las condiciones más sencillas se tiene:

y

Donde :

K Coeficiente de rigidez del resorte (N/m).

C Coeficiente de amortiguamiento viscoso (N-seg/m).

Regresando al modelo discretizado:

5.2.2.- Para un sistema masa-resorte-amortiguador.- En el cual el resorte está conectado a un elemento que sufre un desplazamiento con respecto a su posición de equilibrio.

Si, , se tiene la ecuación de la misma forma que 5.2.1.0.0.1