|
|
|
INTRODUCCIÓN.- Vibración es el termino que utilizamos para describir las oscilaciones de un sistema mecánico. Ella puede ser descompuesta en componentes, cada una de las cuales tiene una magnitud y una frecuencia asociadas. La frecuencia se define en termino de ciclos por unidad de tiempo. La magnitud se define en términos de amplitud. Si la señal sigue un patrón que se repite en el tiempo, hablamos de señal periódica. En caso contrario hablamos de señal compleja.
La vibración es un movimiento oscilatorio en torno a un plano, línea o punto de referencia. Los movimientos vibratorios pueden clasificarse según varios criterios, he aquí algunos:
a) Según el número de grados de libertad
i) Vibraciones de sistemas de un grado de libertad.
ii) Vibraciones de sistemas de múltiples (dos o más) grados de libertad (finitos).
iii) Vibraciones de sistemas de infinitos grados de libertad o continuos.
b) Según las causas que producen el movimiento
i) Vibraciones naturales o libres: producidas por un impulso inicial y luego el sistema no recibe más energía del exterior. Estas vibraciones pueden ser no amortiguadas (teóricamente continuarían al infinito) o amortiguadas
ii) Vibraciones sostenidas o forzadas: producidas en forma continua por la influencia de una fuerza determinista (periódica) o aleatoria, exterior al sistema.
c) Según la forma de la ecuación diferencial del movimiento
i) Vibraciones lineales: cuya ecuación diferencial del movimiento es lineal
ii) Vibraciones no lineales: gobernadas por ecuaciones diferenciales no lineales
d) Según la naturaleza del objeto que vibra
i) Vibraciones de máquinas: sea en su conjunto o de sus elementos constitutivos (árboles, ruedas, álabes de turbinas, palas de helicópteros, resortes, etc.)
ii) Vibraciones de vehículos: sea en su conjunto (automóviles, aviones, buques), sea de sus elementos componentes (alas, hélices, ruedas, etc.).
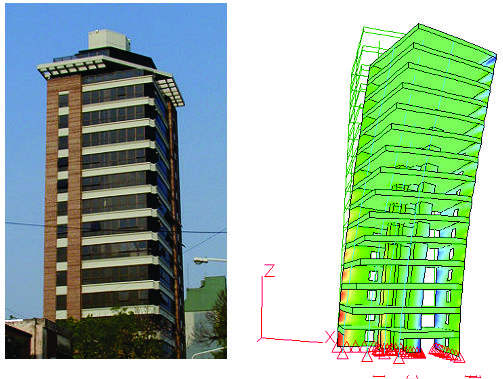
iii) Vibraciones de edificios y otras construcciones civiles.
4i) Otros (líquidos, gases, etc.)
e) Según la naturaleza del movimiento vibratorio
i) Vibraciones de traslación
ii) Vibraciones de rotación
iii) Vibraciones mixtas, etc.
En general, la frecuencia a la cual la energía es entregada al sistema aparece en las respuestas del mismo. La respuesta está dada por la relación que hay entre la excitación y las propiedades del sistema.
Uno de los principales objetivos del estudio de las vibraciones es determinar cuantitativamente la magnitud de las amplitudes de los desplazamientos, velocidades y aceleraciones para constatar si son superiores o inferiores a los límites admisibles. Se tratan entonces de conocer ciertos límites admisibles para los numerosos elementos sometidos a vibraciones.
Las magnitudes características de las vibraciones están limitadas por los factores que a continuación tratamos de exponer:
a) El efecto sobre el hombre
Las vibraciones tienen sobre el hombre efectos nocivos muy variados. Así por ejemplo, las vibraciones muy lentas, características de los buques, pueden provocar el mal de mar. Las vibraciones de los automóviles fatigan y son, a veces, la causa de muchos problemas físicos del cuerpo de los pasajeros / conductores. En los edificios destinados a viviendas u oficinas, las vibraciones son fastidiosas y molestas sobre todo por sus efectos sobre el sistema nervioso. Para el hombre que trabaja en forma permanente en un lugar sujeto a vibraciones - trátese de un conductor de vehículos, de un operario atendiendo una máquina, etc. el efecto nocivo se presenta bajo forma de fatiga, de disminución de la productividad, a la larga también bajo forma de enfermedades profesionales.
Muchos investigadores en diferentes países han estudiado los efectos de las vibraciones sobre el hombre para establecer las condiciones y las escalas de percepción, así como los niveles admisibles de las vibraciones.
b) El efecto sobre los edificios
Las vibraciones producidas en los edificios pueden provocar (además de los efectos sobre hombres y máquinas) daños a la construcción. Se comienza por la destrucción del cielorraso, por los vidrios que se rompen y pueden llegar a fisuras en las fundaciones, los pisos y columnas. El caso extremo está representado por los efectos desastrosos de un terremoto.
Un gran número de estudios revelan los efectos de las vibraciones en los dominios más variados de la técnica, teniendo como punto de partida una gran variedad de factores. La documentación recogida hasta ahora ha permitido realizar algunas síntesis, bajo forma de diagramas y tablas, y que, en ciertos países, revisten carácter de norma obligatoria. No obstante, estas indicaciones no representan todavía una forma universalmente aceptada, sea debido a los límites admisibles adoptados como con relación a la magnitud física utilizada como criterio para apreciar la nocividad. Es por eso que el lector, frente a la documentación técnica presentada, deberá realizar un análisis crítico con respecto a los factores característicos del problema que él mismo debe resolver.
El problema es simple cuando el criterio para apreciar la vibración está representado por la deformación del material provocada por la vibración. En este caso, la resistencia de materiales da la magnitud admisible para la deformación de los cuerpos estudiados, así puede concluirse directamente el límite admisible de la vibración.
|
|
|
|
|
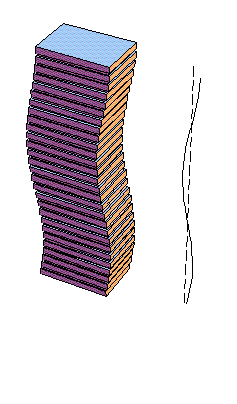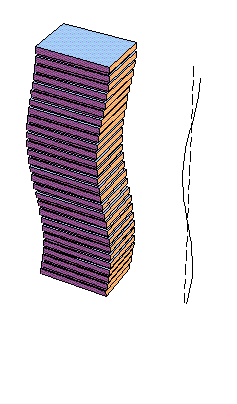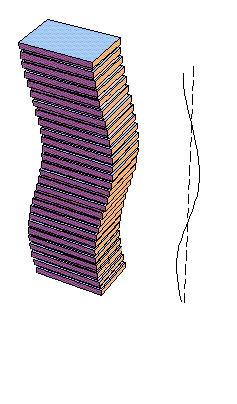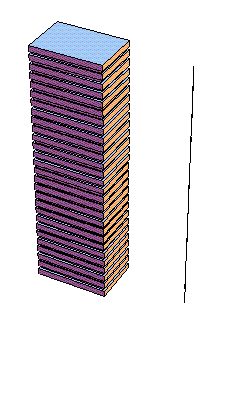
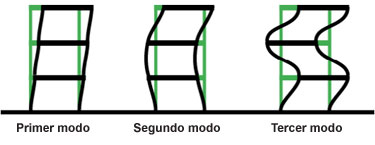
Figura F5-1.1a.- Modos de vibración de un edificio
c) El efecto sobre las máquinas y los aparatos
Los daños que las vibraciones pueden provocar en las máquinas y aparatos revisten varios aspectos. En primer lugar, es necesario considerar los efectos de fatiga mecánica debido a las fuertes vibraciones después de las cuales algunos elementos de máquinas pueden fallar o romperse. Las vibraciones pueden representar un obstáculo para el desarrollo normal de un proceso de fabricación, dando origen a una calidad deficitaria de los productos elaborados (por ejemplo, el caso de vibraciones en máquinas-herramientas). Las vibraciones que llegan a los aparatos de medida pueden ser extremadamente contraproducentes (falsean la medida) cuando están montados a bordo de vehículos.
Recordemos también que las vibraciones pueden ser deseables o no en el funcionamiento de una máquina. Ejemplos de las zarandas vibratorias. Sin embargo lo usual es lo contrario: las vibraciones implican cargas dinámicas extras para un sistema, como es la fatiga.
 |
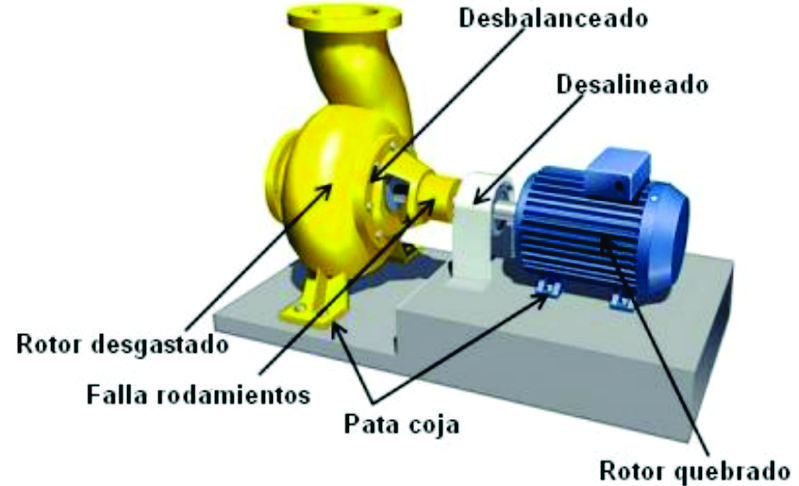 |
Figura F5-1.1b.-Toda Máquina Vibra
El control de las vibraciones puede ser categórizado en 3 grupos:
- Reducción en la fuente: donde esta el balanceamiento de masas en movimiento (ventiladores, motores,..), balanceamiento de fuerzas magnéticas (motores eléctricos), Reducción de juegos (en descansos).
- Aislación: podemos aislar una máquina que genera excesivas vibraciones de modo que no afecte la operación de otras, podemos aislar una máquina sensible a las vibraciones de un ambiente pleno de vibraciones.
- Reducción de la respuesta: alterando frecuencias naturales, incrementando la amortiguación, o añadiendo absorbedores dinámicos.
Para poder analizar en profundidad es necesario conocer las características modales del sistema. Esto es conocido como análisis modal experimental. Se ve, que una vez identificadas las frecuencias naturales y modos propios de una máquina o estructura esta información sera útil para:
- Diagnosticar situaciones de vibración excesiva,
- Rediseñar componentes de estructuras,
- Predecir respuestas a situaciones de carga extremas,
- Estudiar efectos de modificaciones en el comportamiento dinámico de un sistema.
5.1.- SISTEMAS VIBRATORIOS DE UN GRADO DE LIBERTAD
5.1.1.- Introducción.- Vibración es un término usado para describir movimientos de traslación y/o rotación oscilatorios de un cuerpo o de un sistema de cuerpos en direcciones alternativamente opuestas, respecto a su posición de equilibrio estático. A este cambio o movimiento alrededor del equilibrio corresponde una variación de las tensiones internas de los materiales, provocando, en general sobretensión, su fatiga y, a veces, un colapso estructural (resonancia).
Los sistemas vibratorios comprenden elementos para almacenar energía potencial (resorte), elementos para almacenar energía cinética (masa o inercia) y elementos por medio de los cuales la energía se disipa gradualmente (amortiguador). La vibración de un sistema implica la transferencia de energía en sus formas: potencial y cinética. También, la vibración es producto de la interacción activa entre la elasticidad y la inercia del sistema.
Aunque una estructura real o sistema continuo puede almacenar ambas formas de energía y puede también disiparla, en lo que sigue consideraremos sistemas de parámetros concentrados constituidos por resortes, masas y amortiguadores ideales donde cada uno de estos elementos realiza una única función.
También debemos señalar que estudiaremos los sistemas lineales que son aquellos para los cuales la relación entre excitación y respuesta admite el principio de superposición. En otras palabras, el modelo matemático al que responden estos sistemas se traduce en una ecuación de movimiento que es lineal. La linealidad es una hipótesis que está contenida en la formulación matemática del problema y que algunos sistemas responden a ella más que otros dependiendo, en general, de la aproximación deseada de los resultados y del campo de variabilidad de los parámetros que definen el problema. De todos modos, el estudio lineal siempre es importante por cuanto constituye, en muchos casos, una primera aproximación del problema. Sin embargo, conviene subrayar que, en la práctica, efectuar una linealización rápida sin un adecuado control experimental, puede conducir a errores ya que puede carecer de significado práctico asumir la hipótesis de los pequeños movimientos.
En los problemas más simples es posible determinar la configuración de los sistemas mediante una sola coordenada: de ahí que se los conoce como sistemas a un grado de libertad. Es de esta manera como se inicia el estudio de vibraciones.
Las vibraciones son causadas por fuerzas perturbadoras o de excitación (puntuales, aisladas o fluctuantes), que crea en el sistema un desplazamiento con respecto a su posición de equilibrio, los desplazamientos producidos genera un sistema de fuerzas recuperadoras (fuerzas elásticas, como el caso de una masa unida a un resorte o bien fuerzas gravitatorias como el caso del péndulo), que tienden a llevar al sistema a su posición de equilibrio. Al cesar o fluctuar las fuerzas perturbadoras, las fuerzas recuperadores aceleran al sistema hacia su posición de equilibrio, al cual llegan con una velocidad determinada, que hace sobrepasar está posición, de está manera se genera un movimiento vibratorio u oscilatorio, que puede disminuir, mantenerse o aumentar, según se presente o no fuerzas de resistencia o amortiguamiento.
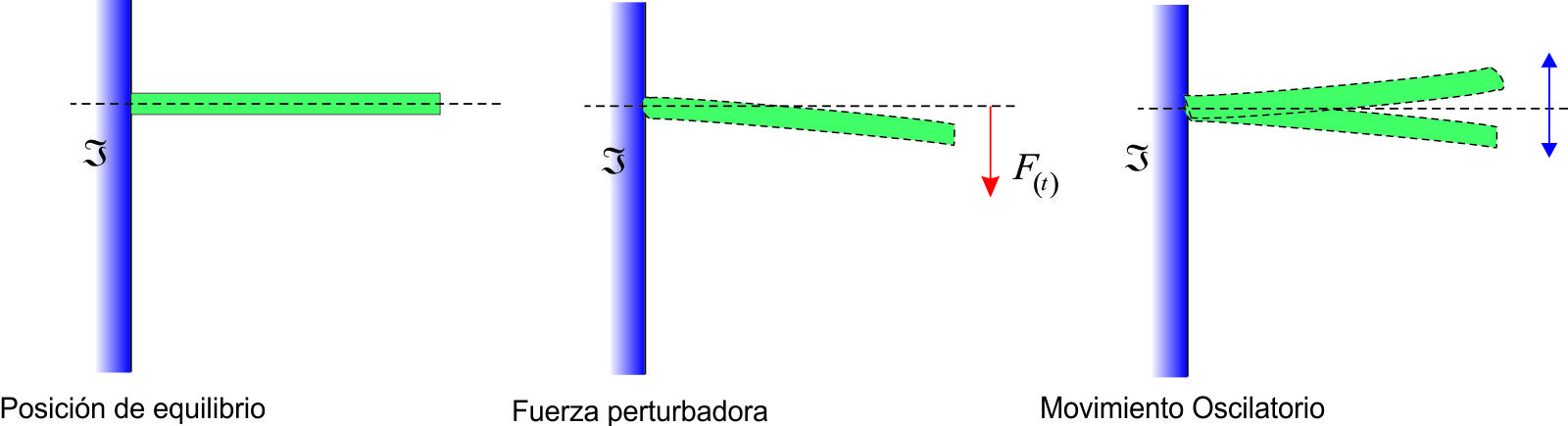 |
|
Figura F5-1.1c.- Cuerpo elástico continuo
|
Los sistemas oscilatorios pueden clasificarse como lineales o no lineales, para los lineales rige el principio de superposición y los términos matemáticos para su tratamiento están bien desarrollados, en contrario para los no lineales son menos conocidos y difícil de aplicarse, sin embargo, algunos conocimientos del sistema no lineal es deseable puesto que todo los sistemas tienden a volverse no lineales cuando crece la amplitud de oscilación.
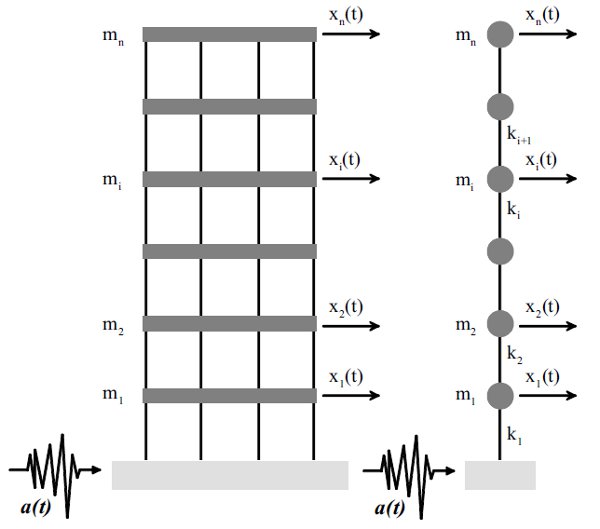
El número de grados de libertad de un sistema, desde el punto de vista de la dinámica, corresponde al número mínimo de coordenadas necesarias para definir la posición en el espacio y en el tiempo de todas las partículas de masa del sistema. Cuando se trata de sistemas rígidos, en los cuales no puede haber desplazamiento relativo entre las partículas de masa, las propiedades de la masa se pueden describir referidas a su centro de masa. Esto conduce a lo que se conoce como sistemas de masa concentrada. Cuando la masa hace parte de un elemento flexible tenemos un sistema de masa distribuida y por consiguiente se puede hablar de un número infinito de grados de libertad.
Para poder describir el movimiento físico de un sistema se necesita elegir un conjunto de variables o coordenadas, las cuales se conocen con el nombre de coordenadas generalizadas. Por regular, se representa mediante el símbolo qk, que dependen de los grados de libertad.
El movimiento de una partícula libre, se describe mediante las coordenadas generalizadas q1 = xp, q2 = yp y q3 = zp. En este caso, las tres coordenadas son necesarias para describir el movimiento del sistema. La cantidad mínima de coordenadas independientes que se requieren para describir el movimiento de un sistema se denomina grados de libertad del sistema. Así, una partícula libre que experimenta un movimiento general en el espacio, tiene tres grados de libertad.
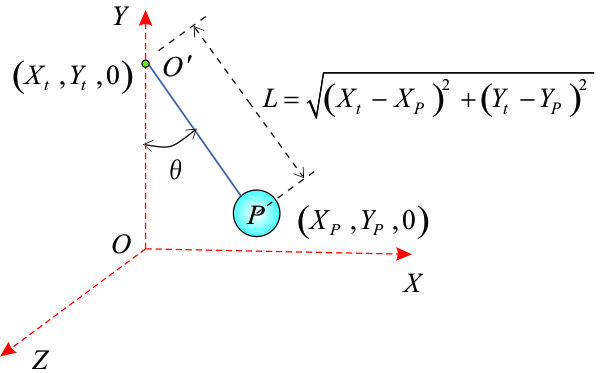
En la figura F5-1.1d se muestra un péndulo en el plano. El punto pivote de este péndulo en (xt, yt, 0) y el péndulo tiene una longitud L. En este caso, se eligen como coordenadas xp y yp. No obstante, como la longitud del péndulo es constante, estas coordenadas no son independiente entre sí porque:
![]()
 |
|
Figura F5-1.1d
|
La ecuación es un ejemplo de una ecuación de restricción, que en este caso, es una restricción geométrica. El movimiento del péndulo en el plano se describe por medio de xp o yp. Como ![]() , entonces se puede utilizar la variable
, entonces se puede utilizar la variable ![]() para describir el movimiento del péndulo, la cual es una coordenada independiente que califica como coordenada generalizada. Como sólo se necesita una variable o coordenada independiente para describir el movimiento del péndulo, un péndulo de longitud constante en el plano tiene un grado de libertad.
para describir el movimiento del péndulo, la cual es una coordenada independiente que califica como coordenada generalizada. Como sólo se necesita una variable o coordenada independiente para describir el movimiento del péndulo, un péndulo de longitud constante en el plano tiene un grado de libertad.
Es necesario tomar en cuenta las ecuaciones restrictivas en la determinación de la cantidad de grados de libertad de un sistema. Por lo que se refiere a la configuración de un sistema especificado por n coordenadas. las cuales están relacionadas con m restricciones independientes, los grados de libertad N están dados por:
![]()
Un cuerpo rígido tiene seis grados de libertad, tres componentes de la posición de un punto base y tres ángulos que definen su orientación. Un cuerpo elástico continuo, requerirá un número infinito de coordenadas (tres para cada punto), para definir su movimiento, por lo tanto tiene infinitos grados de libertad, sin embargo en muchos casos puede suponerse, que partes de dicho cuerpo son rígidos y el cuerpo puede definirse como dinámicamente equivalente a uno con número finito de grados de libertad. Por ejemplo toda estructura continúa tiene un número infinito de grados de libertad. Sin embargo, el proceso de selección o idealización de un modelo matemático apropiado permite reducir los grados de libertad a un número discreto y en algunos casos a uno solo.
Se van a analizar, a continuación, las vibraciones en sistemas mecánicos.
Los objetivos
primarios serán: comprender su naturaleza, estudiar algunos casos sencillos, proporcionar
la base necesaria para acometer el estudio de problemas prácticos más complicados, e
introducir los conceptos y magnitudes utilizados en los modernos equipos de medidas
dinámicas.
Se estudiarán aquí las vibraciones de sistemas con un grado de libertad, al tiempo que se introducen algunos conceptos importantes a los que se hará referencia posteriormente. Los sistemas con un grado de libertad (1 gdl) tienen una excepcional importancia en la Teoría de las Vibraciones porque:
- Son los sistemas más sencillos, lo que hace pedagógicamente necesario comenzar por su estudio.
- Muchos problemas prácticos pueden ser suficientemente aproximados por sistemas con 1 gdl.
- Muchas de las propiedades de estos sistemas se presentan también en sistemas con más grados de libertad.
- Mediante la técnica del "análisis modal" los sistemas lineales con n gdl pueden resolverse superponiendo n sistemas con 1 gdl.
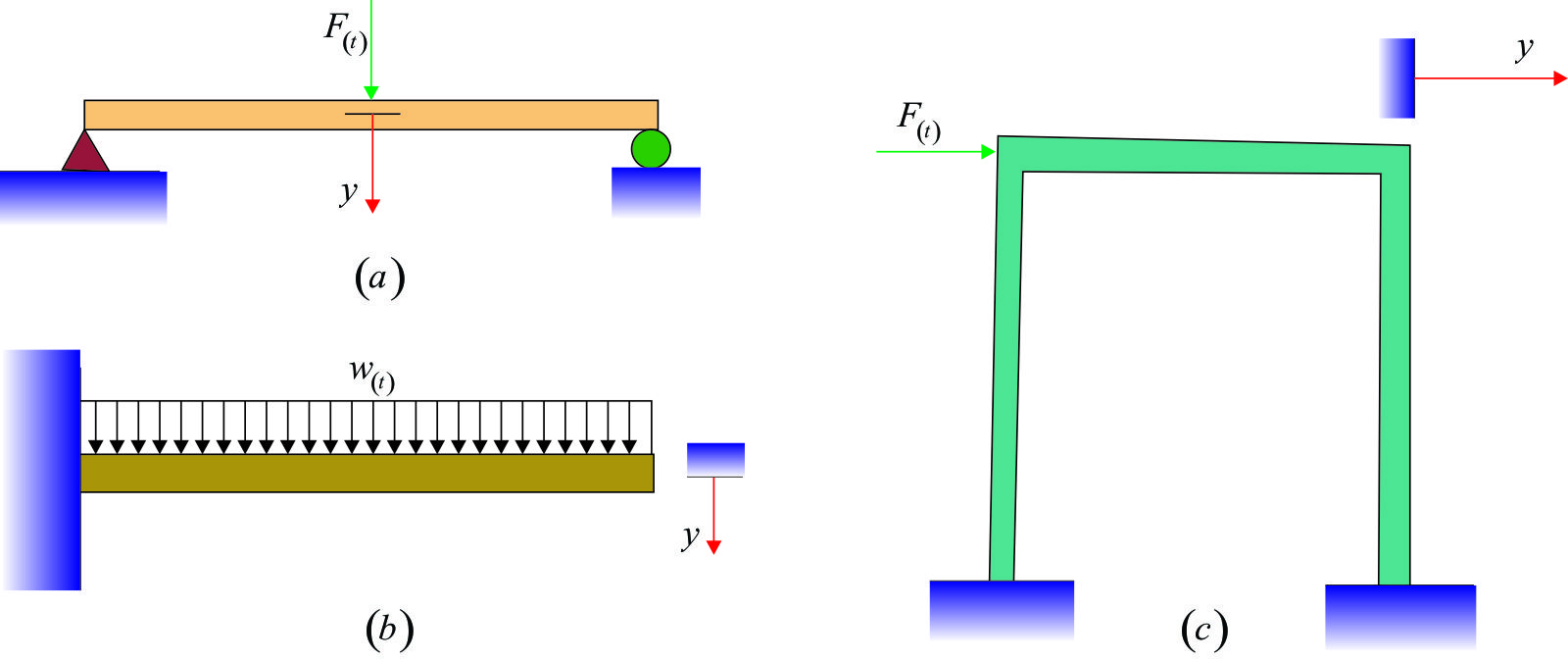
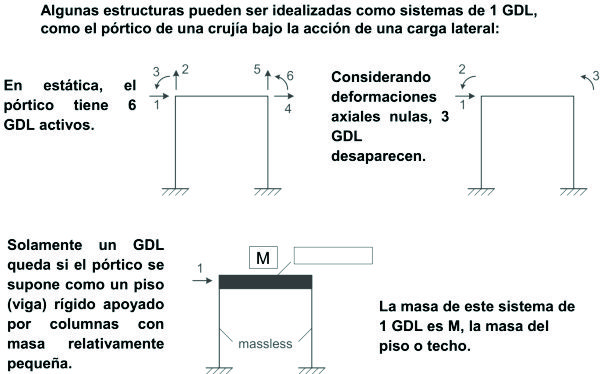
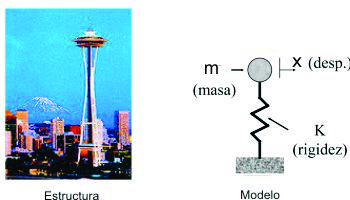
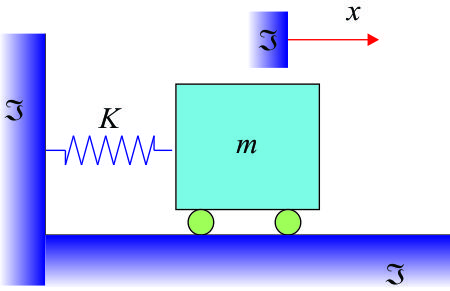
Las figuras F5-1.1d, muestran algunos ejemplos de estructuras que pueden ser representadas como un sistema con un grado de libertad para el análisis dinámico.
|
Estructuras simples: pueden idealizarse como una masa "m" concentrada o agrupada soportada por una estructura sin masa con rigidez "k" en la dirección lateral.
|
|
Figura F5-1.1e |
Ejemplo de movimiento vibratorio
Nota.- Muchos autores diferencian el concepto de vibración y oscilación de la siguiente manera:
Los términos movimiento, oscilación y vibración no son sinónimos. Toda vibración es una oscilación y toda oscilación es un movimiento, pero esta afirmación no puede hacerse en sentido inverso. Así, una rueda se mueve pero no oscila, y un péndulo simple oscila pero no vibra.
La diferencia específica que delimita el significado del concepto de vibración se encuentra, haciendo intervenir el concepto de energía. Tanto las oscilaciones como las vibraciones se prolongan en el tiempo mediante un proceso de conversión entre distintos tipos de energía. Así, en el péndulo simple los tipos de energía que intervienen son la energía cinética y la energía potencial gravitatoria. Pues bien, para que se pueda hablar de vibración de un sistema mecánico es necesario que aparezca un tipo de energía especial la ENERGÍA de DEFORMACIÓN o la ENERGÍA POTENCIAL ELÁSTICA (oelastoplástica).
5.1.2.- Estudio de sistemas sometidos a vibraciones.- En los problemas de ingeniería no es siempre posible obtener soluciones matemáticas rigurosas. En verdad, sólo en algunos casos simples pueden obtenerse soluciones analíticas. Cuando los problemas implican propiedades de materiales, distribución de cargas y condiciones de contorno complejas, es necesario introducir simplificaciones o idealizaciones para reducir el problema a una solución matemática que sea capaz de dar resultados aceptables desde el punto de vista de la seguridad y la economía. El nexo entre el sistema físico y la posible solución matemática se obtiene con el modelo matemático o modelo discretizado, esta es la designación simbólica del sistema idealizado de sustitución que incluye todas las simplificaciones impuestas al problema físico.
|
|
Figura F5-1.2a.- Idealización de un sistema
Cuando el cuerpo o sistema a estudiar se aproxima a un modelo en el cual las masas reales se sustituye por masas concentradas, conectadas por resortes sin masas, el sistema recibe el nombre de "sistemas de parámetros localizados" o modelo discretizado (aquel cuya masa y elementos elásticos están separados o concentrados). En cambio, si se considera la masa del modelo o del sistema en su forma distribuida (son aquellos cuya masa y elementos elásticos están repartidos en el espacio físico), produciéndose una variación continúa del movimiento a través de su masa, se dice que el sistema es de "parámetros distribuidos". Solo estudiaremos el sistema de parámetros localizados
La discretización es ideal para sistemas que se encuentran en movimiento de traslación, pero no así en sistemas cuyos elementos tienen distintos tipos de movimiento, para la cual hay que considerarlos como tal, pero teniendo en cuenta las consideraciones del movimiento de 1 gdl.
5.1.3.- Formulación de ecuaciones del movimiento.- En la formulación se usa distintos métodos, como los que se enumera a continuación:
- Ecuaciones de la Dinámica (Leyes de Newton y Euler)
- Principio de D'Alambert
- Principio de trabajos virtuales
- Teoremas de la energía
- Ecuaciones de Lagrange
- Principio de Hamilton