4.5.- MÉTODOS ESPECIALES PARA EL MOVIMIENTO PLANO DEL CUERPO RÍGIDO.- TRABAJO Y ENERGÍA CINÉTICA, E IMPULSO Y CANTIDAD DE MOVIMIENTO.

4.5.1.- Principio de Trabajo y Energía cinética.-

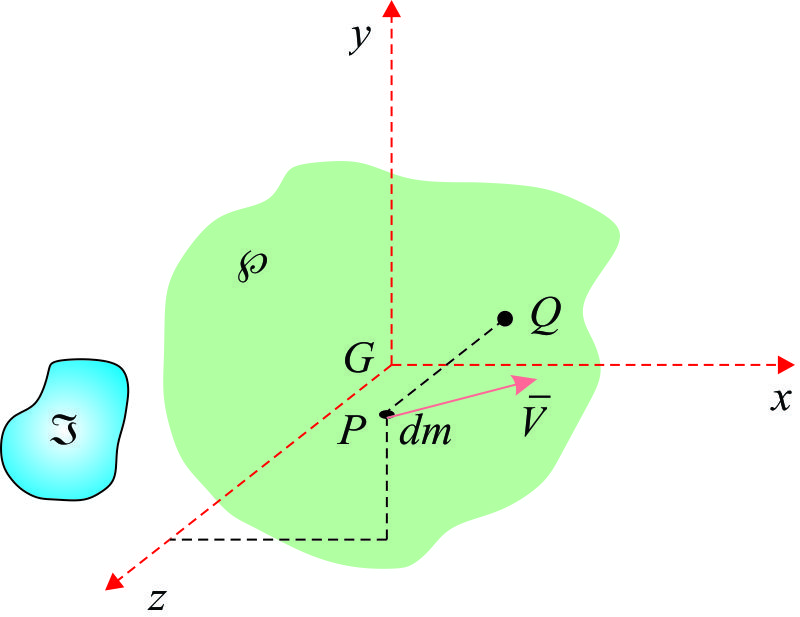
4.5.1.1.- Energía cinética de un cuerpo rígido en movimiento plano:

Sabemos, que:

Si :

Reemplazando en 4.5.1.1.0.1 y operando:

Nota.- Se tiene dos partes identificables (no componentes), una se refiere al movimiento del centro de masa y la otra al movimiento del cuerpo relativo a G

4.5.1.2.- Energía cinética de un cuerpo rígido en movimiento plano, que implica usar el centro instantáneo de velocidad nula.-

En 4.5.1.1.0.2:

Figura F4-5.1.2

Del teorema de los ejes paralelos (Steiner), tenemos en 4.5.1.2.0.1:

También, si:

La ecuación 4.5.1.1.0.1, se puede escribir:

Aplicando la propiedad para el triple producto escalar, , al integrando, obtenemos, , así que la energía cinética es:

Para cuerpos simétricos al plano de movimiento del G:

4.5.1.3.- Deducción del Principio de Trabajo y Energía Cinética : Trabajo y Potencia en Sistema de Fuerzas y Pares.

Derivando 4.5.1.1.0.2, respecto al tiempo:

Nota._ El cambio de la energía cinética en el tiempo, da a lugar a la aparición de la suma de la tasa de trabajo o Potencia (P) debido a las fuerzas y pares.

Sustituyendo en 4.5.1.3.0.1:

Aplicando la propiedad del triple producto escalar, en los pares de el sistema de fuerzas, se tiene:

Como :

Por lo que, desaparecerán las potencias de los pares producidos por el sistema de fuerzas:

Luego :

Nota._ 4.5.1.3.1.1 nos indica, que los momentos producidos por el sistema de fuerzas, no producen potencia (tasa de trabajo).

De 4.5.1.3.0.1, se obtiene el trabajo sobre el cuerpo:

Separando variables e integrando, 4.5.1.3.1.2:

De 4.5.1.3.0.1:

[4.5.1.3.1.4]

4.5.1.3.2.- Para dos cuerpos rígidos y , que forman un sistema y suponiendo, que los cuerpos están conectados por un pasador (o articulación) con fricción despreciable:

Sea :   Fuerza ejercida por sobre . Velocidad común del punto de unión. Potencia de las fuerzas (externas), que actúan en . Potencia de las fuerzas (externas), que actúan en . Energía cinética de . Energía cinética de .

Figura F4-5.1.3.2a

D.C.L.(s):

La ecuación 4.5.1.3.1.1 en y :

y

Sumando ambas expresiones:

Donde:

Potencia de las fuerzas externas ejercidas en el sistema.

Energía cinética del sistema.

Nota.- Si hay fricción en el punto de unión, tendríamos momentos o pares interactivos (desapareciendo si la fricción fuese demasiado grande, en donde ), y la potencia de estos es : ; que en general no es nulo (es negativo), y trae como consecuencia la disipación de energía por fricción.

4.5.1.4.- Trabajo efectuado por diversos tipos de fuerzas y pares.

4.5.1.4.1.- Si, es constante:

4.5.1.4.2.- Si, actúa sobre el mismo punto (del cuerpo ), en su movimiento:

4.5.1.4.3.- Si, es debido a la gravedad (Z es positivo hacia abajo):

4.5.1.4.4.- Si, es la fuerza normal ejercida en el punto de contacto sobre un cuerpo rígido, que mantiene contacto con una superficie fija en , esté el cuerpo rodando o resbalando:

[4.5.1.4.4.1]

4.5.1.4.5.- Si, es la fuerza de fricción ejercida en el punto de contacto, cuando un cuerpo rueda (sin deslizamiento) sobre una superficie fija en :   Si :     [4.5.1.4.5.1]

Figura F-5.1.4.5

4.5.1.4.6.- Si, es la fuerza de un resorte lineal conectado a los mismos dos puntos P y Q de los cuerpos y , durante un intervalo de sus movimientos:

Sea :

K Módulo del resorte.

Longitud sin alargamiento.

Alargamiento ( < 0 representa acortamiento ).

Vector unitario a lo largo del resorte, dirigido hacia el cuerpo .

El trabajo del resorte S sobre el cuerpo es:

[ ]

Si :

Derivándole, con respecto al tiempo:

y sabiendo que:

Sustituyendo en [ ]:

Luego :

4.5.1.4.7.- Fuerzas de un cable inextensible, unidos a dos puntos Q y P de los cuerpos y , durante un intervalo de su movimiento.- El cable en mención, puede pasar sobre una o más poleas ligeras sin fricción, colocados entre los cuerpos, pero deben estar tensos en todo momento. De hecho el trabajo es igual a cero, lo que demostraremos.

Poniendo en términos de sus componentes // y al cable:

Notando, que las componentes perpendiculares a las velocidades, tienen productos escalares nulos con respectivamente; obteniendo los trabajos, por lo tanto, como sigue:

Tomando la diferencial del cable inextensible:

4.5.1.4.8.- Para un par , en 4.5.1.3.0.1 :

Si, el momento en Z es constante, el trabajo del par es:

Nota 1.- Si el trabajo es positivo, nos indica que cuerpo gira en la dirección del momento.

Nota 2.- Para fuerzas conservativas, es valido todo lo deducido para un sistema de partículas.