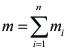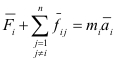III CINÉTICA DE UN SISTEMA DE PARTÍCULAS Y DE CENTRO DE MASA DE CUERPOS
|
3.1.- INTRODUCCIÓN
Los cuerpos que se observan a simple vista están formados por un gran número de partículas, macroscópicas, atómicas o subatómicas. Sólo en ciertos casos es válida la simplificación que supone el modelo de la masa puntual. En otros casos, por el contrario, será necesario considerar el sistema como si estuviese formado por varias partículas.
Se llama Sistema de Partículas, Sistema Mecánico o Sistema Dinámico a un conjunto de varias partículas, de número finito o infinito, de las cuales se quiere estudiar su movimiento.
|
|
Por otro lado:
Se llama Configuración de un Sistema a la posición de cada una de sus partículas en un instante dado.
Para definir la configuración se necesita un determinado número de parámetros según el sistema de que se trate. Por ejemplo, una partícula libre precisa de tres parámetros (x; y; z) que son sus coordenadas Cartesianas. Un sistema de N partículas libres queda definido por 3N parámetros. Sin embargo, si existen ligaduras que restringen el movimiento, el número de parámetros preciso para definir la configuración podría ser menor
En el estudio de un sistema mecánico se prescinde de otras características físicas como la carga eléctrica, color, temperatura, etc.
El movimiento de un cuerpo o sistema de partículas, se relaciona con acciones mecánicas externas (fuerzas y/o momentos), por los cuales las nociones de la cinemática de espacio y tiempo deben ampliarse, con las de masa y fuerza, quienes como las primeras son nociones fundamentales de la mecánica.
Usamos el término cuerpo, para denotar un material de identidad constante.
El punto de partida usual para relacionar las fuerzas externas, que actúan en un cuerpo o sistema de partículas y su movimiento resultante, son las leyes de Newton (Principia 1687), enunciadas solo para partículas, ya que Newton tomo a los cuerpos celestes como partículas y no extendió su trabajo a los problemas, en las que es necesario tomar en cuenta los tamaños reales de los cuerpo y la forma en que está distribuida su masa. Transcurrieron más de 50 años antes de que el matemático Suizo Leonhard Euler presentara el primero de los dos principios, que ha venido a conocerse como las Leyes de Euler.
El estudio se realiza a través de diferentes formulaciones, entre las cuales tenemos:
a).- La mecánica vectorial o newtoniana.- Es una formulación de la mecánica clásica que estudia el movimiento de partículas y sólidos rígidos en el espacio tridimensional, basada en un marco de referencia inercial (sistema de referencia) donde las ecuaciones del movimiento se reducen a las Leyes de Newton, en honor a Isaac Newton quien inicialmente formuló esta teoría.
Esta mecánica es aplicable a cuerpos que se mueven en relación a un observador (marco Inercial) a velocidades pequeñas comparadas con la de la luz. Se basa en que una partícula se mueve dentro de un campo gravitatorio y está sujeta a la acción de la fuerza de este campo, produciéndole una variación de su cantidad de movimiento. El estudio de estas fuerzas y momentos a través de sistemas de referencias inerciales, corresponde al estudio de la mecánica vectorial.
La mecánica vectorial usa tres ecuaciones escalares, o una ecuación vectorial, para el caso de una sola partícula.
Cuando se trata de un sistemade N partículas puntuales, las ecuaciones escalares son 3N, etc.
b).- La mecánica analítica.- Estudia los principales conceptos escalares de la física, entre los cuales tenemos: la energía cinética y el trabajo, tanto en su forma diferencial como integral; y a partir de los cuales se obtienen analíticamente las ecuaciones de movimiento.
La mecánica analítica es más abstracta y general, que usa sistemas inerciales o no inerciales sin que cambie la forma básica de las ecuaciones. La mecánica analítica tiene dos formulaciones: La formulación lagrangiana y la formulación hamiltoniana, que son esencialmente equivalentes, emplean el formalismo de variedades diferenciables, y las dos llegan a los mismos resultados físicos, aun que depende del tratamiento que se da a cada tipo de problema siendo más conveniente un enfoque u otro según el objeto del análisis.
A diferencia de la mecánica vectorial que utiliza 3N ecuaciones siendo N el número de partículas, en la mecánica analítica, siendo el movimiento en varias dimensiones, utiliza una sola ecuación diferencial para estudiar los sistemas mecánicos de acuerdo a las coordenadas generalizadas.
Por otro lado es necesario señalar que, la mecánica lagrangiana describe el movimiento de un conjunto de N partículas puntuales mediante coordenadas generalizadas sobre el llamado espacio de configuración mediante un sistema de N ecuaciones diferenciales ordinarias de segundo orden. En cambio en la mecánica hamiltoniana el movimiento se describe mediante 2N ecuaciones diferenciales de primer orden. El conjunto de transformaciones de coordenadas que permitan resolver el problema es más amplio en la mecánica hamiltoniana.
Se resalta el hecho de que la Mecánica es una ciencia Física, puesto que trata el estudio de fenómenos Físicos. Sin embargo, algunos la asocian con las Matemáticas, mientras que muchos lo consideran como un tema de la Ingeniería. La Mecánica constituye la base de la mayoría de las ciencias ingenieriles y es un requisito indespensable para su estudio. Sin embargo, la Mecánica no tiene el empirismo encontrado en algunas ciencias ingenieriles, esto es, no depende únicamente de la experiencia o de la observación; por su rigor y el énfasis que pone en el razonamiento deductivo se asemeja a las matemáticas. La mecánica no es una ciencia abstracta ni tampoco una ciencia pura; la Mecánica es una ciencia aplicada. El propósito de la Mecánica es de explicar y predecir los fenómenos físicos y, por ende, establecer los fundamentos para las aplicaciones ingenieriles.
El objetivo de la Dinámica es la formulación matemática de las leyes generales que rigen el movimiento de los sistemas materiales.
Consideraciones ha tomar para el estudio de los Sistemas de Partículas.
Sea:
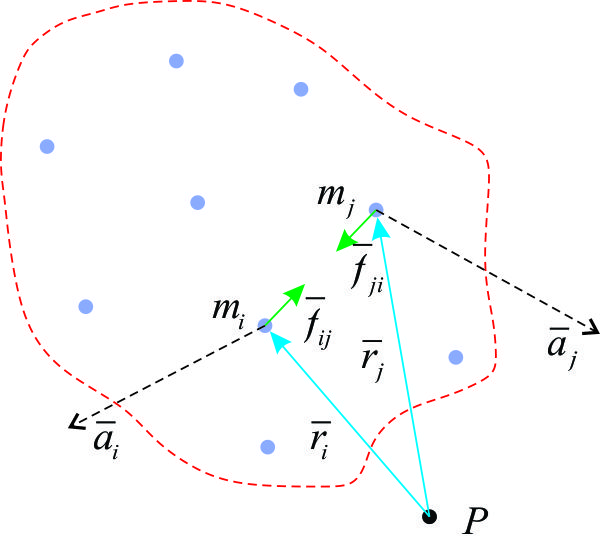
Frontera del Sistema (ver Figura F3-1a) es la envoltura imaginaria que lo encierra y separa de su entorno o exterior. Puede pensarse que la frontera de un sistema de partículas tiene propiedades especiales que sirven para: (a) aislar el sistema de su entorno o para (b) permitir la interacción de un modo específico entre el sistema y su entorno.
Número de partículas aisladas dentro de la frontera (no hay restricción si el sistema es deformable o indeformable).
Masa de la partícula iésima, sometida a fuerzas internas y/o externas.
Fuerza interna o reactiva (fuerza ejercida por la partícula jotésima sobre la partícula iésima).
Fuerza externa (resultante sobre la partícula iésima). En el exterior o entorno del sistema pueden existir agentes que ejerzan influencia sobre el mismo como: campos gravitacionales o eléctricos originados por otro sistema de partículas, sistemas de partículas en contacto con él, etc.

>
Figura F3-1aDinámica de los sistemas de partículas (Recuperado de: https://youtu.be/msWGCJXElLY)
Sistema de particulas: Definiciones previas (Recuperado de: https://youtu.be/e-6n-SxUFc0)
Clasificación de los Sistemas de Partículas
a).- Sistemas discretos.- Sistema de partículas, con número de partículas finitas y éstas están localizadas. En un sistema discreto la masa total del sistema se obtiene sumando las masas de todas las partículas que lo forman; se da por ejemplo, cuando, se desea hacer estudios especiales en las cuales se puede identificar fácilmente a las partículas tales como el sistema solar (sol, tierra).
La ditribución de su masa discreta es:
Dentro de este modelo se consideran:
Sistemas indeformables: Son los sistemas en los que la distancia relativa entre las partículas que lo constituyen permanece inalterable en el tiempo
Sistemas deformables: Son los sistemas en los que puede cambiar la distancia relativa entre las partículas que lo constituyen.
Ejemplo: Usando el mouse(fuerza externa) sobre una de las partículas, vea la acción de repulsión y atracción del las fuerzas internas en las partículas dicretas mostradas.
Ejemplo de movimientos de sistemas discretos : Haga click aquí
b).- Sistemas Continuos.- Sistema de partículas, con número de partículas "infinitas" continuas. Las partículas que lo forman no se pueden delimitar, llenando todo el espacio que ocupa.
La ditribución de su masa continua es:
Al igual que en el caso discreto, dentro de este modelo se consideran:
Sistemas indeformables:
Son los sistemas que no sufren deformaciones por efecto de fuerzas externas, es decir, son sistemas de partículas contínuos cuyas posiciones relativas no cambian. A estos sitemas se les da el nombre de Cuerpo Rígido. Un cuerpo rígido es una idealización ya que, en la naturaleza, todos los cuerpos se deforman en mayor o menor grado bajo la acción de una fuerza externa. Sin embargo, en muchos casos la deformación puede ser tan pequeña que para fines prácticos se puede suponer que no existe. Para el estudio del comportamiento de estos sistemas existe la denominada Mecánica de los Cuerpos Rígidos.
Sistemas deformables:
Son los sistemas que sufren deformaciones por efecto de fuerzas externas, es decir, son sistemas de partículas contínuos cuyas posiciones relativas internas cambian.
En muchos casos prácticos un sistema discreto que tenga un gran número, pero finito, de partículas puede tratarse como un sistema continuo. Inversamente, un sistema continuo puede tratarse como un sistema discreto con un gran número, pero finito, de partículas.
Se da por ejemplo, en:
i) Fluidos.-.- Los aspectos macroscópicos del fluido puede representarse, como modelos donde se agrupan muchas partículas en un sistema simple (volumen de control).
ii) Cuerpos rígidos .- (su estudio se da en el próximo capitulo).
iii) Cuerpos deformables .- Queda fuera del alcance de este capítulo los cuerpos deformables, como es el caso de los materiales elásticos. La consideración de la deformabilidad de los cuerpos exigiría introducir medidas de la deformación interna (tensor de deformaciones), así como de las fuerzas internas entre las partículas del sólido (tensor de tensiones) y las ecuaciones que ligan ambas (ecuaciones constitutivas), lo que excede los objetivos de este curso.
¿Cómo funcionan las Leyes de Newton?, Recuperado de; https://youtu.be/86ZNmoAdlNg
Enunciado de las Leyes de Newton en Flash de I.E.S Juan A. Suanzes
3.1.1.1.- Primera Ley (Principio de inercia).- Todo cuerpo continúa en su estado de reposo o de movimiento rectilíneo y uniforme a menos que sea obligado a cambiar de estado por fuerzas que actúan sobre él.
PRIMERA LEY DE NEWTON (principio de la Inercia, recuperado de: https://youtu.be/e_81dtB8d2Q)
Es equivalente a expresar que "es posible adoptar, por lo menos un marco de referencia, para la cual toda partícula aislada continua en su estado de reposo o de movimiento rectilíneo y uniforme".
Recuerde se denomina partícula a todo cuerpo cuyas dimensiones y orientación resultan despreciables en la descripción de su movimiento.
A los sistemas de referencia en reposo o se desplaza con movimiento rectilíneo y uniforme (es decir no acelerado) respecto a un marco de referencia, se les denomina Sistemas de referencias Inerciales.
Una partícula aislada es aquella que no interactúa con otras o sea, no esta afectada por las acciones ("fuerzas") que estas pudieran ejercer sobre ella.
3.1.1.2.- Segunda Ley (Principio de masa o Ley Fundamental de la Dinámica).- La derivada de la cantidad de movimiento respecto al tiempo es proporcional a la fuerza que actúa sobre el cuerpo y tiene su dirección y sentido.
La que es equivalente a expresar: "Una partícula a la que se aplique una fuerza acelera en la dirección de la fuerza en el marco inercial o primario. La magnitud de la aceleración es proporcional a la magnitud de la fuerza e inversamente proporcional a la masa de la partícula".
k = 1, para unidades cinéticas coherentes o sistemas cinéticos. Donde no es posible elegir arbitrariamente las unidades de: fuerza, masa, longitud y tiempo (si se elige tres, la cuarta se elige de modo que satisfaga la ecuación, lo que nos dice que las unidades de fuerza, masa y aceleración son dependientes).
Es una ley puramente experimental y su significado fundamental se describe con ayuda de un experimento ideal en el cual se supone que la fuerza y la aceleración se miden sin error.
Ejemplo: Cambio de la Fuerza Resultante en un Péndulo Simple
Pincha sobre Tarzán, sepáralo de su posición de equilibrio y pulsa play, se genera un movimiento armónico simple. Se representan las componentes intrínsecas de la aceleración y las fuerzas que actúan sobre Tarzán. Se puede añadir rozamiento al movimiento.
Ejemplo: Cuerpo moviéndose en un círculo vertical
3.1.1.3.- Tercera Ley (Principio de acción y reacción).- A toda acción ejercida sobre una partícula, se opone una reacción igual y de sentido contrario que ejerce la propia partícula.
Se refiere a la interacción entre dos partículas y en otras palabras señala que toda vez que una partícula ejerce una fuerza sobre otra, ésta ejerce sobre la primera una fuerza de igual intensidad y dirección pero de sentido contrario.
Nota 1.- Es claro, que la primera Ley puede considerarse como un caso especial de la segunda y que, debe hacerse "una suposición respecto al marco de referencia", ya que un punto puede tener velocidad constante en un marco y variable en otro.
Nota 2.- Los marcos de referencia en las que estas leyes son validas, se denomina Galileanas, Newtonianas, astronómicas, primarios o inerciales (no usaremos el termino absoluto por ser una apreciación particular), estos marcos de referencia son imaginarios, que suponen carentes de rotación y traslación en el espacio o son marcos de referencia en traslación con velocidad constante respecto al marco primario.
Sistemas no Inerciales en Flash
Nota 3.- Las discrepancias, cuando se toma como marco de referencia a la tierra, es que se debe tomar correcciones debida a la aceleración de la tierra respecto a otros marcos. En la mayoría de los problemas técnicos referente a movimientos de estructuras y máquinas en la superficie terrestre, las correcciones son despreciables, por lo que, lo consideramos como marco primario.
Nota 4.- En la Mecánica Newtoniana el espacio, el tiempo y la masa son conceptos absolutos e independientes entre sí (esto no es cierto en la mecánica relativista, donde el tiempo de un evento depende de su posición y la masa de un cuerpo varía con su velocidad). Por ota parte, el concepto de fuerza no es independiente de las tres.
3.1.1.3.- Primera Ley.- Para un sistema de partículas la suma de las fuerzas externas, que actúan sobre el sistema es igual a la suma de los productos masa iésima por la aceleración iésima
de las partículas que forman el sistema; deducida a partir de la segunda ley de Newton.
a).- Segunda Ley de Newton para la partícula iésima:
D.C.L. de la partícula iésima (ver figura F3-1.2.1a)
Se sabe que:
b).- Para el sistema de Partícula:
.
Si:
(acción y reacción)
Figura F3-1.2.1a
c).- Para un cuerpo cuya masa está distribuido en forma continua la ecuación 3.1.2.1.0.2 se convierte en:
Si:
es un elemento diferencial de masa,
es su aceleración y
es la suma de las fuerzas externas que actúan sobre el cuerpo

F3-1.2.1c
d).- Para sistemas conformadas por subsistemas discretos la ecuación 3.1.2.1.0.2, se escribe refiriéndose a los centros de masa de los subsistemas, de la siguiente manera:
3.1.2.2.- Segunda Ley.- Para un sistema de partículas, la suma de los momentos de las fuerzas externas respecto a un punto es igual a la suma de los momentos de
respecto al mismo punto.
a).- En 3.1.2.1.0.1 formamos el producto vectorial de
con ambos miembros de la ecuación:
b).- Para el sistema:
Figura [F3-1.2.2]
Los términos,
en la doble suma, aparecen en parejas, pero sabemos que,
, ya que,
y
tienen una línea de acción común, que pasa por las partículas "1" y "2", además
, por lo que concluimos, que :
; cumpliéndose también para las demás parejas de partículas.
Luego en 3.1.2.2.0.2:
c).- Para un cuerpo con masa distribuida en forma continua, la ecuación 3.1.2.2.0.3 se convierte en:
Nota 1.- 3.1.2.1.0.2 y 3.1.2.2.0.3 juegan el mismo papel en la dinámica, que
y
en la estática.
Nota 2.- Para la solución de un problema en particular, se tiene 3 alternativas: a) aplicación de las leyes de Eueler, b) utilización de los métodos energéticos o c) métodos de la cantidad de movimiento e impulso.
Leer el Capitulo III del Libro