4.4.- ESTUDIO DEL MOVIMIENTO EN EL PLANO DEL CUERPO RÍGIDO.
4.4.1.- Movimiento en traslación:
![]() (de toda las partículas)
(de toda las partículas)
|
[4.4.1.0.0.1]
|
|
[4.4.1.0.0.2]
|
y |
[4.4.1.0.0.3]
|
|
[4.4.1.0.0.4]
|
Ejemplo de movimiento en traslación:
Se dibujan las fuerzas internas y externas que actúan sobre un sistema formado por un camión y su carga. Se pueden variar el coeficiente de rozamiento y la fuerza externa aplicada.
4.4.2.- Movimiento alrededor de un eje fijo en un marco inercial (punto base "O" en el eje):
|
[4.4.2.0.0.1]
|
|
[4.4.2.0.0.2]
|
De 4.3.1.3.0.3:
|
[4.4.2.0.0.3]
|
Para cuerpos simétricos, con el plano de movimiento de "G":
|
[4.4.2.0.0.4]
|
Ejemplo: Caida de una barra
4.4.3.- Movimiento General en el Plano:
|
[4.4.3.0.0.1]
|
|
[4.4.3.0.0.2]
|
Para los momentos, se utiliza cualquiera de las ecuaciones deducidas
Si, el cuerpo es simétrico, con respecto al plano de movimiento del centro de masa "G" y/o la resultante de las cargas externas tiene su línea de acción en el plano de movimiento del centro de masa "G", usamos:
|
[4.4.3.0.0.3]
|
a).- Disco con movimiento de rodadura o con deslizamiento.- Si no se sabe con certeza si el disco está deslizando o no; la condición para no deslizamiento (rodadura) deberá suponerse y comprobarse primero. Cuando la fuerza de fricción tiene una magnitud ![]() no existe deslizamiento y la suposición fue correcta. Por otra parte si
no existe deslizamiento y la suposición fue correcta. Por otra parte si ![]() indica que existe deslizamiento. La solución debe iniciarse de nuevo con
indica que existe deslizamiento. La solución debe iniciarse de nuevo con ![]() ahora conocido, pero
ahora conocido, pero ![]() y
y ![]() no están relacionados.
no están relacionados.
b).- Rotación de cuerpos desbalanceados o inequilibrados.- Hay dos causas, que desequilibran a un cuerpo en rotación:
i).- La primera, es que el centro de masa se localiza a una distancia, fuera del eje de rotación. Al girar el cuerpo, aparecen fuerzas en los apoyos (cojinetes), igual a ![]() , estás fuerzas cambian constantemente en dirección (respecto al marco inercial), si es, que no en magnitud.
, estás fuerzas cambian constantemente en dirección (respecto al marco inercial), si es, que no en magnitud.
ii).- La segunda causa del desbalanceo es la presencia de los productos de inercia ![]() y/o
y/o ![]() , en donde "z" es el eje de rotación y "A" un punto sobre ese eje.
, en donde "z" es el eje de rotación y "A" un punto sobre ese eje.
|
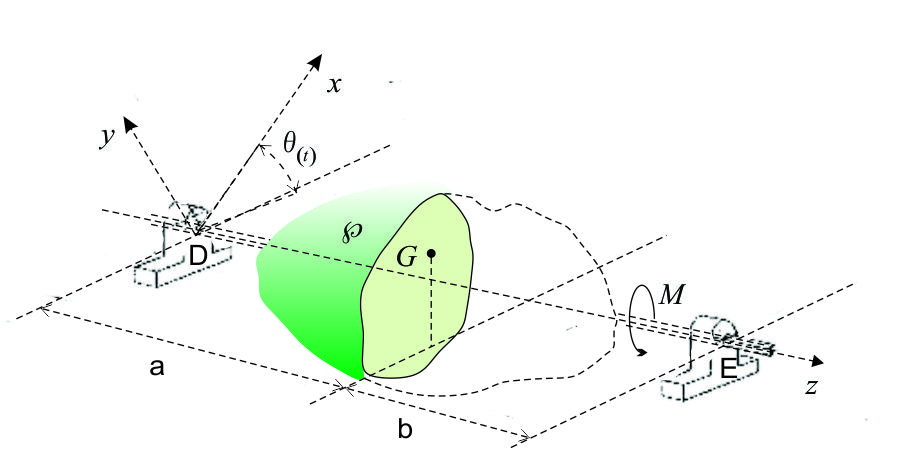
Para balancear, podemos añadir o quitar material, para forzar que los productos de inercia sean nulos; cuando se hace esto, además se asegura que el centro de masa "G" se encuentre sobre el eje, luego se dice que el cuerpo está dinámicamente balanceado y por su puesto estáticamente también, que demostraremos como sigue.
Sea:
|
|
*).- D.C.L. (omitiendo los efectos de la gravitación en el análisis):
|
|
|
Figura F4-4.4b
|
**).- Relaciones Cinemáticas:
![]()
![]()
***).- Relaciones Cinéticas (no consideramos el peso):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Observamos, si se conocen: ![]() , las propiedades geométricas y de inercia del cuerpo, se podrá obtener las reacciones
, las propiedades geométricas y de inercia del cuerpo, se podrá obtener las reacciones ![]() , y
, y ![]() pero, para balancear al cuerpo estás fuerzas dinámicas deben desaparecer ; de tal manera que:
pero, para balancear al cuerpo estás fuerzas dinámicas deben desaparecer ; de tal manera que:
![]()
![]()
Esto se consigue aumentando (contrapeso) o quitando masa al cuerpo ; si aumentamos y conocemos del cuerpo desbalanceado ![]() , ("P" punto cualquiera localizado en el eje de rotación); determinaremos las coordenadas
, ("P" punto cualquiera localizado en el eje de rotación); determinaremos las coordenadas ![]() y
y ![]() de las masas
de las masas ![]() y
y ![]() (pequeños para tratarlos como partículas),en dos planos correctivos A (en
(pequeños para tratarlos como partículas),en dos planos correctivos A (en ![]() ) y B (en
) y B (en ![]() ) para que, el cuerpo quede balanceado. De la siguiente manera:
) para que, el cuerpo quede balanceado. De la siguiente manera:
|
[1]
|
|
[2]
|
|
[3]
|
|
[4]
|
Si, conocemos:
|
[5 y 6]
|
Balanceamos al cuerpo con estas seis ecuaciones.
Ver animación de equlibrado dinámico de movimiento de una particula sobre un eje fijo