Cuando un cuerpo se sujeta a un movimiento general en el plano, experimenta una combinación de una traslación y una rotación. La traslación ocurre dentro del plano de referencia y la rotación alrededor de un eje perpendicular al plano de referencia a través del punto base o conveniente.

2.5.3.1.- Estudio del Movimiento:

Sea: XY el plano de referencia en .

En (4) , (5) y (6) , se tiene:

(10)

 

(11)

 

(12)

 

Analizando las dos últimas ecuaciones (11) y (12):

: conocidos, por ser el punto base o conveneiente.

: Sus direcciones son conocidas.

: De hecho es conocido.

Conclusión: Se tiene tres incógnitas para cada ecuación, pudiendo dar cada una dos ecuaciones, al igualar componentes; para poder solucionar los problemas recurrimos a los tres métodos más conocidos, que son el: Vectorial, geométrico y escalar.

2.5.3.2.- Método vectorial.- Para este método se usa la ecuación general de la cinemática del cuerpo rígido, para la cual debe conocerse la dirección de la velocidad y de la aceleración de la partícula cuyo movimiento se desconoce o en caso contrario debe conocerse el movimiento angular del cuerpo rígido. Por lo que debe utilizarse las ecuaciones (10), (11) y (12).

2.5.3.3.- Método geométrico.

2.5.3.3.1.- Centro instantáneo de velocidad nula.- Si “P” es un punto en el plano de referencia, con velocidad nula en algún instante, entonces el campo de velocidades del cuerpo rígido , es lo mismo, como si el cuerpo estuviese obligado en ese instante a girar alrededor de un eje a través de P, normal al plano de referencia. Tal eje se denomina “eje instantáneo de rotación” y al punto P se le llama centro instantáneo (C_i) de velocidad nula de . Así, si Q es cualquier otro punto de (ver figura) se tendrá:

o bién:

Por ejemplo se tiene el campo de velocidades de una rueda en rodamiento, en la figura siguiente:

Determinación del centro instantáneo (C_i) de velocidad nula:

a).- Rodamiento.-

Sea:

y dos cuerpos rígidos en movimiento. Decimos que existe rodamiento entre y , si durante su movimiento:

*).- Una sucesión continua de puntos, sobre la superficie de entra en contacto biunívoco (uno a uno) con una sucesión de puntos sobre la superficie de .

**).- En todo instante durante su movimiento, los puntos en contacto tienen el mismo vector velocidad, lo que nos indica, que no puede haber resbalamiento o deslizamiento entre los puntos de las superficies de y para que exista rodamiento (ver figura).

Nota.- Muchos autores usan la frase "rodamiento sin deslizamiento", para describir el movimiento de "rodamiento".

Consideramos tres clases de problemas que implican contacto de rodamiento:

i).- Rodamiento de una rueda , sobre una línea fija en

Sea:

la rueda, que está rodando sobre el terreno (marco de referencia inercial en este caso). Puesto que los puntos de están todos en reposo, el punto de contacto de , es de hecho el centro instantáneo de velocidad nula (ver figura).

También:

Luego, la aceleración del centro instantáneo de velocidad nula es:

Ejemplo: Sobre un plano horizontal, con su respectivo cicloide de la partícula ha considerar.

ii).- Rodamiento de una rueda sobre una curva plana fija en

*).- Superficie cóncava hacia arriba:

Sea:

y vectores unitarios tangencial y normal principales para el punto central "G" de la rueda (ver figura).

Figura F2-5.3.3d

Puesto, que sucesivamente estamos definiendo el movimiento, tal que el punto de contacto, tenga velocidad nula (C_i), se tiene:

Derivandole, con respecto al tiempo en el marco inercial, se tiene:

Sabemos:

Luego la aceleración de C_i es:

Para Q:

**).- Superficie cóncava hacia abajo:

Figura F2-5.3.3e

Derivandole, respecto al tiempo en el marco inercial tierra:

También sabemos:

Luego:

Es útil considerar la siguiente fórmula, que no depende de ninguna elección particular de un sistema de coordenadas:

(parte normal)

Si conocemos o la componente tangencial de , por ejemplo, podemos obtener la otra sin preocuparnos por expresar la componente normal de .

Ejemplo: Rodamiento sobre curvas concavas

iii).- Movimiento de engranajes conectados.- Los engranajes, se usan para transmitir potencia. Sus dientes engranes se perfilan de modo que impartan velocidad constante al engrane impulsado, cuando el engrane impulsor gira a velocidad angular constante (ver figura del ejemplo de engranajes rectos de ejes fijos).

Sin embargo, los engranes violan la condición de rodamiento, por que, existe necesariamente algún resbalamiento, ya que los puntos de contacto no tienen velocidades iguales (excepto en , donde se encuentran los circulos de paso), como puede verse en la figura, no obstante, los dientes se cortan de modo que podemos tratarlos correctamente para fines dinámicos como si fueran dos cilindros rodando uno sobre otro, en sus circunferencias de paso o base, por ejemplo tenemos lo mostrado para dos engranajes con ejes fijos en , para la que usamos las relaciones siguientes:

Notándose que la relación de los radios es inversamente proporcional a la relación de las velocidades angulares (y directamente proporcionales a la relación del número de dientes).

Nota.- Si bien las velocidades de los puntos de contacto en los rodamientos tienen las mismas velocidades, pero no así las aceleraciones son iguales, lo que, es si, las aceleraciones tangenciales son iguales en dichos puntos de contacto.

Ejemplo de rodamiento de engranajes

b).- Cuando se conoce las direcciones no paralelas de las velocidades de dos puntos A y B.- El centro instantáneo “c_i” se encuentra en la intersección de las líneas perpendiculares a las direcciones de las velocidades, trazadas por dichos puntos (ver figura).

c).- Cuando las velocidades de los puntos A y B son paralelas.- Para poder determinar el centro instantáneo “c_i” es necesario conocer además de las direcciones, los módulos y sentidos de las velocidades. “c_i” se obtiene de la intersección de las líneas que pasan por los puntos A y B, y la que une los extremos de los vectores velocidades. Si las líneas son paralelas todas las partículas tendrán la misma velocidad, que no implica necesariamente que el cuerpo este en movimiento de traslación (es instantáneo) (ver figuras).

Figura F2-5.3.3h

d).- Por linealidad de los centros instantáneos o polos inerciales.- Cuando dos o más cuerpos están unidos por un punto común, se puede hallar un centro instantáneo para cada cuerpo, que en general no coinciden.
Como la velocidad del punto (centro instantáneo relativo o polo relativo), que une los cuerpos es la misma para cada uno de ellos, los centros instantáneos de uno y otro deben estar sobre una recta que pasa por el punto común de ambos cuerpos (ver figura).

Figura F2-5.3.3i

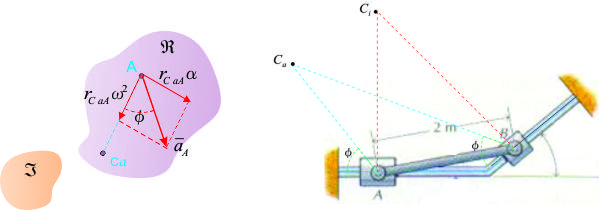
2.5.3.3.2.- Centro instantáneo de aceleración nula.- Análogo al centro instantáneo de velocidad cero, existe otro centro instantáneo de aceleración cero, de tal manera, que se pueda encontrar la aceleración de un punto cualquiera como si el cuerpo estuviese moviéndose alrededor de un eje instantáneo, que generalmente no coincide con el de la de la velocidad cero, salvo caso especifico (ver figura).

a).- Método general para la obtención del centro instantáneo de aceleración nula.-

Lo que nos dice que, para encontrar C_a es necesario conocer y para encontrar el ángulo , luego trazar las líneas correspondientes y así obtener el “C_a”, que hace que no sea práctico su utilización.

b).- Caso especifico.- Cuando el cuerpo parte del reposo (), el ángulo , que hace que “c_i” (no existe) y “c_a” coincidan ().

2.5.3.4.- Métodos escalares.

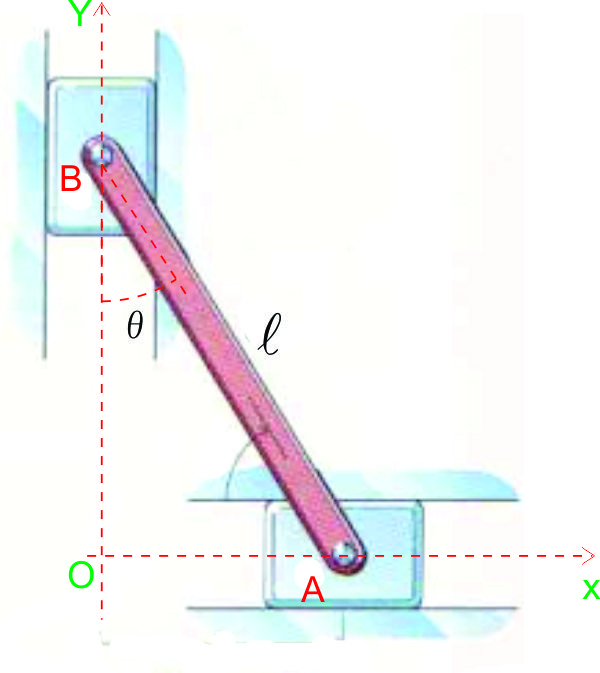
a).- Análisis del movimiento plano en términos de un parámetro.-

En el caso de ciertos mecanismos es posible expresar en las coordenadas X e Y los puntos significativos, por medio de expresiones analíticas simples que contienen un solo parámetro.
Por ejemplos tenemos, el siguiente mecanismo, donde debe conocerse el movimiento de uno de sus puntos (base).

Figura F2-5.3.4

Si:

Derivandoles, dos veces con respecto al tiempo:

Nota.- Muchas veces se utiliza este método solo, para encontrar el movimiento angular; para luego regresar al método vectorial.

b).- Métodos equipotencial.

Estableciendo relaciones que ligan las distintas variables del movimiento del sólido rígido , en un estado general.

i).- Condición de rigidez.

La condición de rigidez la podremos expresar por:

ii).- Condición cinemática de velocidades.

Referenciando al sólido rígido respeto de un punto de referencia "O" quedará:

es el vector diferencia entre vectores posición de los puntos A y B.

Derivándole respecto al tiempo:

iii).- Condición cinemática de aceleraciones.

Derivando (13) respecto al tiempo:

Dividiendo (14) por :

O sea que la proyección de la aceleración en el punto B sobre la dirección es igual a la proyección de sobre la misma dirección menos el cuadrado del modulo de la velocidad relativa dividida por la distancia que separa los puntos.

Ejemplo de combinado de los tres movimientos

Trnsformación de Movimiento

Ejemplo general

Cinemática del Movimiento del Cuerpo Rígido en Movimiento Plano (Recuperado de https://youtu.be/C3TZhGQVTEs)