2.5.2.- Movimiento alrededor de un punto fijo en
.
Es un movimiento en el espacio con desplazamiento alrededor de un punto fijo.
|
|
|
|
Ejemplo de movimiento alredor de ejes fijos y punto fijo en un marco de referencia en particular, de un diferencial de un vehículo.
¿QUE ES UN DIFERENCIAL Y CÓMO FUNCIONA? (Recuperado de https://https://youtu.be/OlnKPyvTxAc?si=6SPNKgvJtD8e7ltc)
2.5.3.1.- Estudio del Movimiento.- Para este movimiento el
punto base es de hecho el punto fijo en
<
Nota.- El movimiento angular, como vector es instantáneo, se da en el espacio
2.5.4.1.- Composición de rotaciones en uniones.
2.5.4.1.1.- Unión de rótula.- Las rótulas permiten
cualquier giro, por lo que es muy difícil conocer la dirección de la velocidad angular
de la barra rótula (AB) (ver figura), pero se le puede descomponer en tres componentes
mutuamente ortogonales:
paralela a AB y
contenidos en un plano perpendicular a AB de modo que:
no se puede determinar,
salvo que se tenga condiciones adicionales sobre ella. En algunos casos para determinados
tipos de uniones, éstos imponen esta velocidad, en caso contrario se asume que, ésta es
nula por no transmitir movimiento angular.
Figura F2-5.4.1.1
Las mismas consideraciones, se toma para la aceleración angular.
2.5.4.1.2.- Unión de horquilla y corredera.- La corredera permite que la
barra gire y deslice, es decir que la velocidad angular (); tenga,
una componente
() en la dirección
del eje de la corredera
(
)
y la segunda (
)
en la dirección del pin que une la horquilla a la corredera
(
)
, de tal manera que no tenga ningún movimiento angular el la dirección perpendicular al
plano (
)
formado por 
(ver figura).
Luego:
También:
|
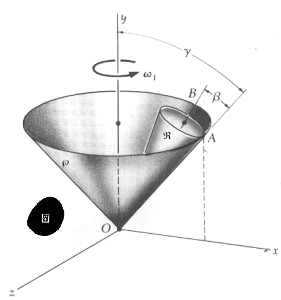
2.5.4.2.3.- Utilizando las propiedades de la velocidad angular.- Se tiene que utilizar estas propiedades, en función del problema en particular que se nos presenta. Un ejemplo lo representa un cono que rueda sobre un plano. Podemos ver este movimiento como una rotación instantánea en torno a la recta de contacto entre el cono y el plano [pues los puntos de contacto tienen velocidad nula y forman el EIR (Eje Instantáneo de Rotación)] pero también puede verse como una composición de dos rotaciones, una en torno a un eje vertical y otra en torno al eje del cono. |
|
|
2.5.4.2.4.- Determinando el eje instantáneo de rotación en un marco de referencia en particular.- El eje instantáneo de rotación (EIR) está formado por los puntos que tienen velocidad nula respecto al marco donde se realiza el estudio. Consiste en una recta que pasa por de los puntos en reposo instantáneo y tiene la dirección de la velocidad angular. Como los ejemplos que se da: |
|
|
a).- Rodamiento de un Cono
Como ejemplo, tenemos el caso específico, que se muestra en la figura, en donde OA es
fijo a
i).- Por la cinemática, la Velocidad del punto fijo “A” es
Donde:
|
|
en
(
|
ii).- Por el teorema de adición de las velocidades angulares (ver figura), se tiene:
|
|
|
b).- Determinado el eje de rotación instantáneo (EIR).- Siempre debe haber un eje instantáneo en un movimiento de un cuerpo rígido, muchas veces llamado eje de reducción, donde las velocidades de su puntos respecto al marco donde se determina, deben ser nulas en el instante considerado, por lo que la dirección de la velocidad angular debe está en la dirección de dicho eje. Como ejemplo, tenemos el caso específico, que se muestra en la figura F2-5.4.2.4d, cuyo tenor es la que sigue.
Una esfera de radio R (sólido "2"), se desplaza sobre dos carriles circulares concéntricos fijos de radios R y 2R (sólido "1"), situados en un plano horizontal (ver figura). El movimiento de la esfera es tal que: i) en todo instante, rueda sin deslizar sobre ambos carriles, y ii) su centro C realiza un movimiento circular uniforme (antihorario), siendo v0 el módulo de su velocidad. Calcular, para el instante en que C se encuentra en el plano YZ (xyz ligado a la esfera):
La velocidad y aceleración angulares de la esfera, respecto al marco inercial (sólido "1").
Solución
1).- Determinación de la velocidad angular de la esfera respecto al marco inercial.- Como los puntos A y B tienen las velocidades igual a cero respecto al marco inercial, la línea que los contiene será el eje instantáneo o sea el eje "y".
|
|
|
Si:
|
|
(Unidades de velocidad angular)
2).- Determinación de la aceleración angular.- Derivando (1) respecto al tiempo:
Figura F2-5.4.2.4e
|
(2)
|
Si:
|
(3)
|
Luego en (3):
En (2):
(Unidades de aceleración angular)
Nota.- Para la aceleración angular se tiene que tomar en cuenta, en la derivada respecto al tiempo de las velocidades angulares (componentes), en los marcos de referencia que están definidas.
Ejemplo de rodamiento de un cono sobre otro cono fijo
Ejemplo de rodamiento entre conos
 |
 |
 |
 |
Inicio