|
2.1.2 Consideraciones elementales
a).- Una partícula tiene posición, velocidad y
aceleración.
b).- Una cuerpo rígido tiene orientación, velocidad angular y aceleración angular.
|
|
c).- Un punto P del espacio no pertenece a un sólido en concreto, sino a todos ellos simultáneamente.
|
Para poder visualizar este concepto ponemos el ejemplo del mecanismo biela-manivela. El movimiento de este sistema transcurre en un plano, por lo que podemos prescindir de la tercera coordenada (perpendicular al plano). El sistema se compone de tres sólidos: la barra fija (sólido 1), la manivela (sólido 0) y la biela (sólido 2).
A cada uno de ellos podemos asociar un marco de referencia en un plano. Podemos imaginar estos marcos de referencia como hojas de papel superpuestas. Habrá una hoja de papel pegada a la barra. Sobre ella una hoja de papel unida a la manivela y sobre ésta una tercera hoja unida a la biela. Cada hoja se extiende a todo el plano. En cada instante, cada hoja se mueve respecto a las otras dos, aunque sigan superpuestas.
Un punto P del plano lo podemos imaginar como un alfiler que, en un instante dado, atraviesa simultáneamente las tres hojas de papel, de forma que tenemos un agujero en cada uno de las hojas, por ello decimos que el punto P está en los tres sólidos, aunque tenga vectores de posición diferentes en cada uno.
|


|
|
|
Cuando los sólidos se mueven unos respecto a los otros, la posición del punto P puede permanecer fija en alguno de los sólidos, pero cambiar en los otros. El punto P tendrá velocidad nula en uno de los sistemas de referencia y distinta de cero en los otros dos. Habrá situaciones, como el punto de articulación de la biela y la manivela, que tendrá velocidad nula en los sólidos 0 y 2, pero que estará en movimiento respecto al sólido 1.
Observemos que podemos hallar el estado de movimiento de, por ejemplo, la articulación de la biela con la barra, considerando esta articulación como parte del sólido 0 (la manivela) pese a que físicamente este punto no forme parte de la manivela. Debemos imaginarnos unos ejes solidarios con la manivela que llegan hasta este punto y determinar cómo se mueve un punto fijo en este marco de referencia cuando la manivela efectúa sus movimiento de rotación respecto a la barra (o respecto a la biela).
En un sistema tridimensional la idea es exactamente la misma, aunque en lugar de hojas de papel superpuestas deberíamos imaginar volúmenes coincidentes que se mueven de distinta manera. Dado que esta idea es difícil de concebir, nos conformaremos con dibujar sistemas de ejes en movimiento relativo, pero manteniendo siempre en mente que los sólidos no son solo los ejes, sino todo el espacio.
|
|
|
|
2.1.3 Deslizamiento, rodadura y pivotamiento.
|
|
Cuando tenemos dos sólidos en contacto, tales que un punto 2 del sólido 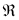 , que se encuentra sobre la superficie del sólido , que se encuentra sobre la superficie del sólido 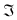 (por ejemplo, una pelota sobre una mesa), es posible que el punto de contacto esté en reposo relativo (revolución instantánea), o que no lo esté. Cuando el punto de contacto posee una cierta velocidad se dice que existe deslizamiento entre los sólidos. Se define la velocidad de deslizamiento entre los sólidos como la del punto de contacto, (por ejemplo, una pelota sobre una mesa), es posible que el punto de contacto esté en reposo relativo (revolución instantánea), o que no lo esté. Cuando el punto de contacto posee una cierta velocidad se dice que existe deslizamiento entre los sólidos. Se define la velocidad de deslizamiento entre los sólidos como la del punto de contacto,  . .
Esta velocidad será necesariamente tangente a la superficie y por tanto ortogonal a  , el vector normal a la superficie. , el vector normal a la superficie.

Por otra parte, la velocidad angular puede tener una de sus componentes en la dirección perpendicular a la superficie, esto es, el sólido 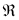 posee un giro en torno a un eje perpendicular a la superficie y paralelo, por tanto, al vector posee un giro en torno a un eje perpendicular a la superficie y paralelo, por tanto, al vector  . Cuando esto ocurre se dice que el sólido . Cuando esto ocurre se dice que el sólido 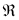 pivota sobre pivota sobre 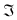 y esta componente de la velocidad angular se denomina velocidad angular de pivotamiento ( y esta componente de la velocidad angular se denomina velocidad angular de pivotamiento ( ). ).

|

|
Además de la posible parte perpendicular a la superficie, la velocidad angular posee una parte tangente a la superficie (y perpendicular a  , por tanto), de forma que el sólido , por tanto), de forma que el sólido 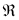 posee una componente de giro a en torno a un eje paralelo a la superficie. Se dice entonces que tenemos rodadura en el punto de contacto, siendo la velocidad angular de rodadura ( posee una componente de giro a en torno a un eje paralelo a la superficie. Se dice entonces que tenemos rodadura en el punto de contacto, siendo la velocidad angular de rodadura ( ). ).
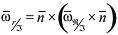
En un movimiento general tendremos las tres componentes: deslizamiento, rodadura y pivotamiento, siendo la velocidad de cualquier punto del sólido 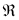 . .
| Deslizamiento
|
Rodadura
|
Pivotamiento
|

|

|

|
|
No obstante, en muchas ocasiones algunas de estas componentes son nulas. Así, tenemos los casos:
2.1.3.1 Rodar y pivotar sin deslizar.
La velocidad de deslizamiento es nula:

El movimiento instantáneo del sólido 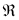 es una rotación pura en torno a un cierto eje que pasa por el punto de contacto. Este es el movimiento que describe habitualmente, por ejemplo, un cono que se mueve sobre una superficie horizontal con rozamiento suficiente para no permitir el deslizamiento. es una rotación pura en torno a un cierto eje que pasa por el punto de contacto. Este es el movimiento que describe habitualmente, por ejemplo, un cono que se mueve sobre una superficie horizontal con rozamiento suficiente para no permitir el deslizamiento.
|
|
2.1.3.2 Rodar sin deslizar (rodadura).
Si no se indica que existe pivotamiento, se supone que este es nulo, en este caso, la velocidad angular  es tangente a la superficie del sólido es tangente a la superficie del sólido 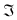 . El movimiento relativo es una rotación pura alrededor de un eje tangente a la superficie de . El movimiento relativo es una rotación pura alrededor de un eje tangente a la superficie de 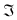 . Este es el movimiento de un disco que rueda sobre un plano. Así, respecto al suelo, una rueda de un coche no rueda en torno a su eje, sino en torno a un eje que pasa por el punto donde toca el suelo y es tangente a este: . Este es el movimiento de un disco que rueda sobre un plano. Así, respecto al suelo, una rueda de un coche no rueda en torno a su eje, sino en torno a un eje que pasa por el punto donde toca el suelo y es tangente a este:

2.1.3.3 Deslizamiento sin rodadura.
La velocidad angular es nula (se supone que tampoco hay pivotamiento) y el sólido 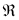 se traslada respecto al se traslada respecto al 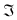 , luego todo los puntos del sólido , luego todo los puntos del sólido 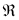 , tienen la misma velocidad y aceleración con respecto al marco , tienen la misma velocidad y aceleración con respecto al marco 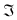 . .
Esto ocurre, por ejemplo, cuando se arrastra un cierto sólido (una caja, por ejemplo) sobre otro.
Ejemplos:
1).- Deslizamiento o rodadura (rodamiento) de un disco sobre un plano horizontal.
2).- Deslizamiento y/o rodadura de un disco sobre un plano inclinado.
|
|