3.2.- ECUACIONES DE MOVIMIENTO PARA EL CENTRO DE MASA DE UN SISTEMA DE PARTÍCULAS.-

 

Recordando:

 

Cálculo y movimiento del centro de masas (Recuperado de: https://youtu.be/XG7IsqCkytY)

 

Se tiene que tener bien en claro, al centro de masa parciales, en muchos casos veremos, es conveniente subdividir el sistema de partículas y hallar los centros de masas de cada subsistema, para luego hallar el centro de masas del conjunto.

 

 

(a) Centro de masas de un sistema de partículas (b) Centros parciales de cada subsistema.

 

 

b).- Sustituyendo en la ecuación 3.1.2.1.0.2, la aceleración de la partícula iésima:

 

 

La posición del centro de masa "G" de un sistema de partículas se define, por:

 

, donde

 

Luego:

 

 

constante (no hay masa que entre o salga del sistema)

[3.2.0.0.0.1]

 

Obtención del Centro de masas, velocidad y aceleración del centro de masas, en forma detallada:

 

Recuperado de: https://youtu.be/zTcxoqbneoc

 

Nota.- La ecuación 3.2.0.0.0.1 establece que el centro de masa de un sistema de partículas, se mueve como si todas las masas de las partículas estuvieran concentradas en el centro de masa, como una sola partícula y bajo la acción de la resultante de las fuerzas externas, que actúan sobre el sistema.

 

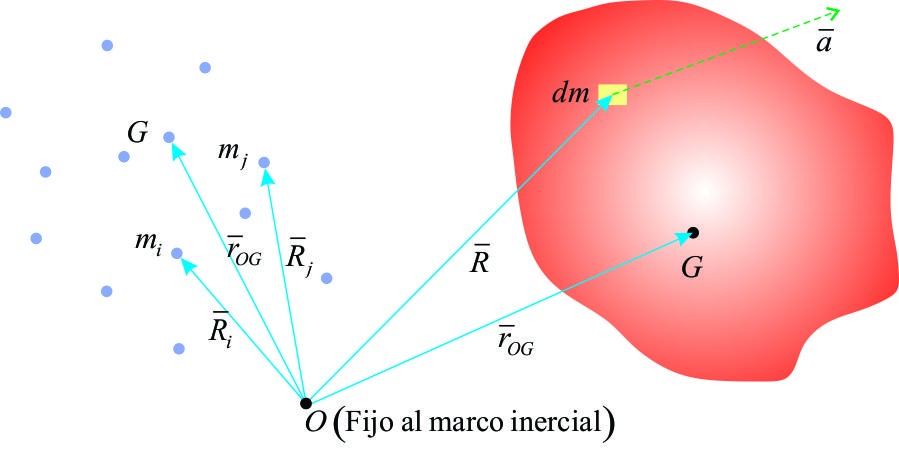
a).- Para un cuerpo con masa distribuida en forma continúa:

 

 

Sabemos también, que:

 

 

Luego:

 

[3.2.0.0.0.2]

 

 

Nota.- Para un cuerpo rígido el centro de masa G, coincide en todo instante con un punto específico del cuerpo o con una extensión rígida del mismo; que no es el caso para los cuerpos deformables.

 

d).- Conservación del movimiento del centro de masa: La resultante de los momentos lineales del sistema es nula si y solo si la resultante de las fuerzas externas es nula

 

Si:

 

 

En 3.2.0.0.0.1:

 

 

Luego:

 

constante

 

El centro de masa está en movimiento rectilíneo con rapidez constante con respecto al marco de referencia inercial.

 

Si, se tiene que , entonces constante.

 

Puede darse en una de sus componentes, tal como:

 

constante

 

Pudiéndose darse también, que constante.

 

Dinámica de los sistemas de partículas (1) Conservación cantidad movimiento y centro de masas

 

Recuperado de: https://youtu.be/YStWPtMGKGg