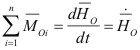3.5.- SEGUNDA LEY DE EULER EN TÉRMINOS DE LA CANTIDAD DE MOVIMIENTO ANGULAR (IMPETU ANGULAR, MOMENTO CINÉTICO O MOMENTUM ANGULAR).-
3.5.1.- Momentum Angular para un sistema de partículas.-
3.5.1.1.- Para la partícula iesima respecto a un punto fijo "O" en 
:
|
[3.5.1.1.0.1]
|
Ejemplo de Momento cinético de una particula respecto a un punto fijo : Haga click aquí
3.5.1.2.- Para el sistema de partículas, respecto a un punto fijo "O" en :
|
[3.5.1.2.0.1]
|
Dinámica | Cinética de Sistemas de Partículas | Cantidad de Movimiento Angular
3.5.1.3.- Para el sistema de partículas, respecto a un punto móvil "A":
Sea:
|
A |
|
en 
El Momentum angular (inercial), es:
|
[3.5.1.3.0.1]
|
El Momentum angular relativo, es:
|
[3.5.1.3.0.2]
|
3.5.1.4.- Para el sistema de partículas, con respecto al centro de masa:
|
[3.5.1.4.0.1]
|
Si:
|
[3.5.1.4.0.2]
|
Nota .- Las Cantidades de movimiento angular con respecto al centro de masa inercial y relativa son iguales.
3.5.1.5.- Relaciones de 
con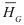 
:
Si: 
|
[3.5.1.5.0.1]
|
Si: 
|
[3.5.1.5.0.2]
|
3.5.2.- Utilizando la segunda Ley de Euler.-
3.5.2.1.- Por la forma fundamental de la segunda Ley de Euler:
|
[3.5.2.1.0.1]
|
3.5.2.1.0.1 nos da la segunda Ley de Euler, en términos del momentum angular.
Si: 
Luego:
|
[3.5.2.1.0.2]
|
3.5.2.2.- Momento respecto al punto arbitrario "A":
Si:
Derivándole este último, respecto al tiempo:
|
[3.5.2.2.0.1]
|
Si:
|
[3.5.2.2.0.2]
|
Para el momentum angular relativo, tenemos:
|
[3.5.2.2.0.3]
|
El estudio del momento se simplifica, si:
a).- 
, para 
; esto, se da cuando:
i).- A 
Es un punto fijo en 
ii).- G Es un punto fijo en
iii).- A Es el centro de masa 
De 3.5.1.4.0.1:
|
[3.5.2.2.0.4]
|
4i) 
b).- 
, para 
; esto, se da cuando:
i).- A Es un punto fijo en
ii).- A Es el centro de masa.
iii).- 
Es constante.
3.5.3.- Impulso Angular y Momentum Angular a un punto fijo o al centro de masa:
Separando variables e integrando:
|
[3.5.3.0.0.1]
|
Ejemplo: Encontrar el movimiento del mono y los platanos, para distintas condiciones.
Conservación del momentum angular:
|
[3.5.3.0.0.2]
|
Constante
Nota.- Cuando se estudia medios continuos más complejos como la dinámica de fluidos con transferencia de calor y compresible, debemos satisfacer cuatro leyes básicas: a) Conservación de la masa, b) Cantidad de movimiento lineal y cantidad de movimiento angular, c) Primera ley de la termodinámica y d) Segunda ley de la termodinámica, que son independientes entre sí (es decir deben satisfacer por separado).
 |
 |
 |
 |
Inicio