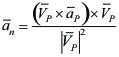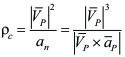Cinemática de una partícula

1.4.2.4.- Fórmulas usuales

a).-

b).-

y (proyecciones)

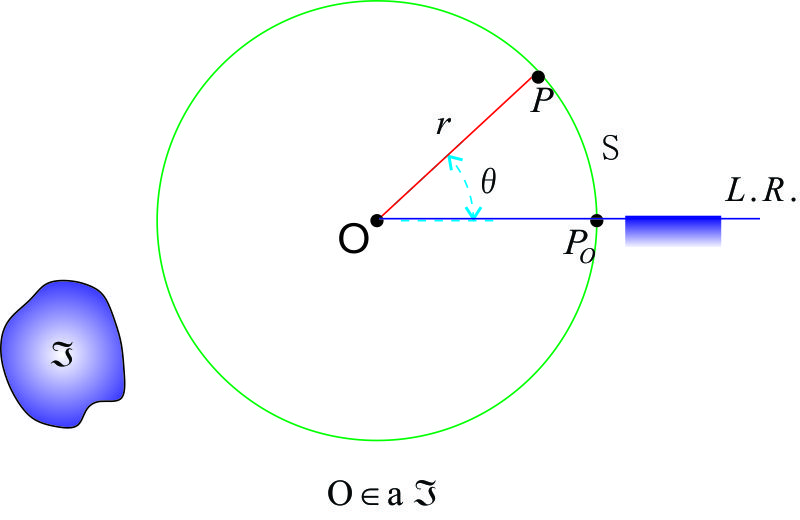
c).- Movimiento de trayectoria circular.- Es un caso particular del movimiento curvilíneo plano, en el cual el radio de curvatura es constante e igual al radio r de la circunferencia de su trayectoria.

Figura F1-4.2.4

Luego:

Ejemplo: Movimiento Circular uniformente acelerado.

Definición: movimiento rectilíneo y periódico que se obtiene al proyectar un movimiento circular uniforme (m.c.u.) sobre un diámetro cualquiera de la trayectoria.

Ecuacion horaria:

Terminología específica:

Elongación

amplitud (máxima elongación)

fase inicial

fase

frecuencia angular o pulsación

período

Ecuacion diferencial:

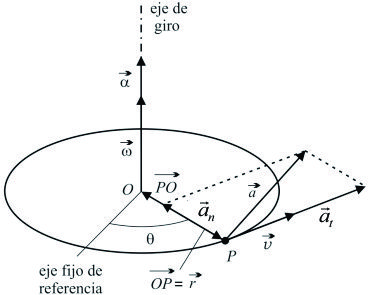
e).- Movimiento helicoidal uniforme (m.h.u.).

Definiciones:

Movimiento de un punto que recorre una hélice con velocidad de módulo constante;

Movimiento que resulta de la superposición de un movimiento circular uniforme (m.c.u.) en un plano y de un movimiento rectilíneo uniforme (m.r.u.) a lo largo de una recta normal a dicho plano.

Ecuaciones cartesianas horarias:

f).- Movimiento central.

Se dice que el movimiento de un punto P es un movimiento central si existe un punto fijo O* (centro del movimiento), tal que la recta soporte del vector aceleración, , del punto P pasa en todo instante por dicho punto O*.

Matemáticamente, si llamamos al vector de posición relativa de P respecto a O*, la condicion de movimiento central viene dada por:

Es importante advertir que el centro del movimiento, O*, no ha de coincidir necesariamente con el origen de coordenadas, O. Precisamente eso es lo que pretende subrayar el uso del asterisco en nuestra notación:

Sin embargo, con vistas a posteriores razonamientos, conviene observar que, al ser O* un punto fijo, se verifica (cuando P se desplaza) que:

g).- Radio de curvatura:

* Cuando : X = X_(t) y Y = Y_(t)

* Cuando : Y = Y_(X)

* En forma general

h).- Fórmulas en general:

De los Acápites anteriores se deduce que, conocida la posición como función del tiempo, , puede calcularse el resto de magnitudes.

No obstante, a menudo no se dispone de una función sino, por medidas experimentales o por otras razones, de los valores de la posición , la velocidad y la aceleración , en un instante dado. En este caso no podemos calcular ninguna derivada (que requiere conocer la dependencia temporal). ¿Quiere esto decir que no podemos hallar la aceleración tangencial, por ejemplo? No. De hecho, empleando los resultados anteriores, podemos calcular los valores de casi todas las magnitudes para ese instante.

Datos	Rapidez	Vector tangente	Aceleración tangencial (vector)	Aceleración tangencial (escalar)

Aceleración normal (vector)	Aceleración normal (escalar)	Vector normal	Radio de curvatura	Centro de curvatura

Como vemos, ninguno de estos cálculos requiere hallar ninguna derivada.

Inicio