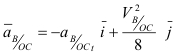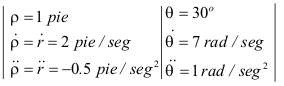La barra delgada y curva OC gira alrededor de O. En el instante que se muestra, la velocidad angular de OC es 2 rad/seg y su aceleración angular es cero. Encuentre la aceleración angular de la barra AB en la misma posición.

Solución

Como el Movimiento no depende del punto de referencia sino del marco de referencia, encontraremos el movimiento de "B", tomando como puntos de referencia a "O" y "A", para luego igualarlos. Para el movimiento con respecto a "O" usaremos movimento en marcos móviles, siendo el marco móvil la barra curva OC y para el movimiento con respecto a "A" , vemos que "B" tiene una trayectoria circular.

1).- Cálculo de la velocidad y aceleración de B tomando como punto de referencia a "O" en _.

a).- Cálculo de la velocidad y aceleración de B' (B' a OC coincidente con B), ver figura P1-9a:

c).- Cálculo de la velocidad y aceleración de B respecto al marco inercial Tierra:

Luego:

2).- Cálculo de la velocidad y aceleración de B, tomando como punto de referencia a "A" en _. :

(1) = (3) e igualando componentes:

(2) = (4):

rad/seg² (antihorario)

En el instante que se ilustra, el brazo AB gira en torno del rodamiento fijo con una velocidad angular = 2 rad/seg y una aceleración angular = 6 rad/seg². En el mismo instante, la varilla BD gira en relación con la varilla AB a = 7 rad/seg, que se incrementa a = 1 rad/seg². Además, el collarín C se mueve sobre la varilla BD con una velocidad = 2 pie/seg y una desaceleración = 0.5 pie/seg² ambas, medidas con relación a la varilla. Usando coordenadas cilíndricas en la varilla AB, determine la velocidad y aceleración del collarín en ese instante.

  

2).- Cálculo del movimiento del marco móvil AB, de la velocidad y aceleración del punto base B:

  

  

(rad/seg)

  

  

(rad/seg²)

  

(pie/seg)

  

  

(pie/seg²)

  

3).- Cálculo del movimiento de C respecto al marco móvil AB.

  

a).- Identificación de los parámetros que definen el movimiento en AB:

  

  

b).- Movimiento de C:

  

(pie)

  

(pie/seg)

  

  

(pie/seg²)

  

4).- Cálculo de la velocidad y aceleración de C en el marco inercial tierra:

  

  

Donde:

  

(pie/seg)

Luego:

  

(pie/seg)

  

(pie/seg)

  

  

Donde:

  

(pie/seg²)

  

(pie/seg²)

  

(pie/seg²)

  

Luego:

  

(pie/seg²)

  

(pie/seg²)

  

(pie/seg²)