Ejemplo Nº E_05
La barra AB gira en sentido contrario al de manecillas del reloj, con una velocidad angular constante de 2 rad/seg. Usando coordenadas natural y/o polares, determine la velocidad del punto C localizado sobre el doble collarín, cuando
. El collarín
consiste de dos bloques deslizadores que están restringidos a moverse a lo largo de la
flecha circular y de la barra AB.
Figura P1-5
Solución
1).- Orientación de los vectores unitarios que definen las coordenadas pedidas:
Figura P1-5a
2).- Cálculo de la velocidad de C, usando coordenadas polares y poniendo sus vectores unitarios en función de los vectores unitarios de la coordenada Natural:
|
(1)
|
3).- Cálculo de la velocidad de C, usando coordenada Natural:
|
(2)
|
(2) = (1), igualando componentes y operando:
Ejemplo Nº E_06
|
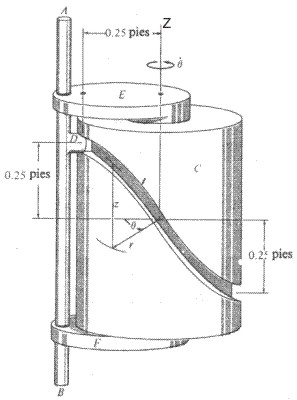
La leva cilíndrica C se mantiene fija mientras la barra AB y los
apoyos E y F giran alrededor del eje Z de la leva con rapidez de
Solución
1).- Por las Características geométricas que presentan, solucionaremos
el problema utilizando coordenadas Cilíndrica.
Figura P1-6a
2).- Cálculo de la velocidad y aceleración de D:
|
|
rad/seg. Si la barra está
libre para deslizarse a través de los apoyos, determine la magnitudes de la velocidad y
la aceleración de la guía D sobre la barra como función de
. La guía sigue la
ranura de la leva, y la ranura está definida por las ecuaciones r = 0.25 pies y
(pies).
" cualquiera (ver figura P1-6a):
 |
 |
 |
 |
Inicio