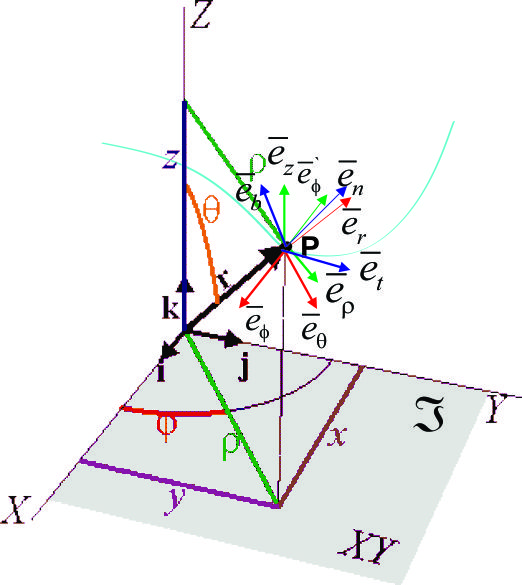
1.3.- MOVIMIENTO EN DISTINTOS SISTEMAS DE COORDENADAS RESPECTO
A UN MARCO DE REFERENCIA INERCIAL
|
Según las características geométricas de cada problema, será conveniente en cada caso escoger uno u otro sistema de coordenadas. La elección obvia en el caso más general será un sistema de coordenadas cartesianas; sin embargo en ocasiones es ventajoso emplear otras coordenadas, como las coordenadas cilíndricas (o polares en el caso plano), esféricas, o el triedro intrínseco a la trayectoria (coordenada natural). En cada uno de estos casos, el aspecto que nos ocupa es obtener las composiciones de los vectores velocidad |
|
y aceleración 
.
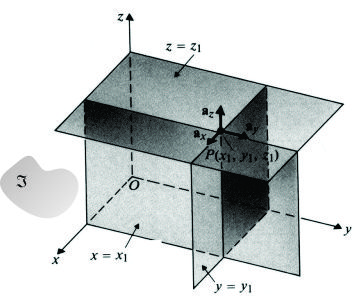
1.3.1.- Movimiento en coordenadas Cartesianas
 |
 |
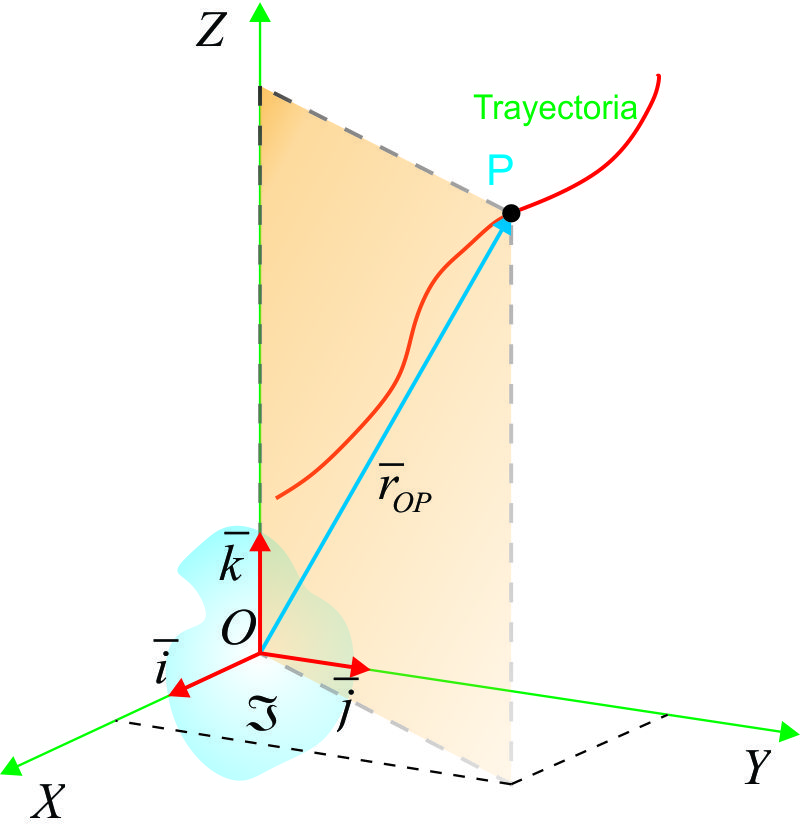
Sea:
P 
Una Partícula
OXYZ Sistema de coordenadas
"ligado o pegado al marco de referencia inercial"
X = X(t) , Y = Y(t) y Z = Z(t)
 |
|
F1-3.1
|
)
|
1.3.1.3.- Vector Aceleración
(
|
 F1-3.2
|
 |
 |
 |
 |
Inicio